Câu hỏi
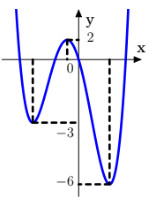
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình bên. Gọi \(S\) là tập tất cả các giá trị nguyên dương của tham số \(m\) để hàm số \(y = \left| {f\left( {x - 2018} \right) + m} \right|\) có \(5\) điểm cực trị. Tổng tất cả các giá trị của tập \(S\) bằng
- A \(9\)
- B \(7\)
- C \(12\)
- D \(18\)
Phương pháp giải:
- Tìm số cực trị của hàm số \(y = f\left( {x - 2018} \right) + m\), từ đó suy ra điều kiện để hàm số bài cho có \(5\) điểm cực trị.
- Từ đó suy ra giá trị của \(m\) thỏa mãn bài toán.
Lời giải chi tiết:
Hàm số \(y = f\left( {x - 2018} \right) + m\) có \(3\) điểm cực trị nên để đồ thị hàm số \(y = \left| {f\left( {x - 2018} \right) + m} \right|\) có \(5\) điểm cực trị thì đường thẳng \(y = 0\) phải cắt đồ thị hàm số \(y = f\left( {x - 2018} \right) + m\) tại đúng \(2\) điểm (không bao gồm các điểm cực trị của đồ thị hàm số \(y = f\left( {x - 2018} \right) + m\)).
Nói cách khác, đường thẳng \(y = - m\) cắt đồ thị hàm số \(y = f\left( {x - 2018} \right) \) tại đúng \(2\) điểm (không bao gồm các điểm cực trị của đồ thị hàm số \(y = f\left( {x - 2018} \right)\)).
Quan sát đồ thị ta thấy \(\left[ \begin{array}{l} - 6 < - m \le - 3\\ - m \ge 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}3 \le m < 6\\m \le - 2\end{array} \right.\).
Mà \(m\) nguyên dương nên \(m \in \left\{ {3;4;5} \right\}\).
Vậy tổng các giá trị của \(m\) thỏa mãn là \(3 + 4 + 5 = 12\).
Chọn C.







