Phương pháp giải:

Xác định chiều cao hình chóp: \(\left\{ \begin{array}{l}\left( P \right) \bot \left( Q \right)\\\left( P \right) \cap \left( Q \right) = a\\d \bot a;\,d \subset \left( P \right)\end{array} \right. \Rightarrow d \bot \left( Q \right)\)

Gọi \(E\) là trung điểm của \(AD\) ta chỉ ra mặt cầu ngoại tiếp hình chóp \(S.ABC\) cũng là mặt cầu ngoại tiếp hình chóp \(S.EABC\) .

Từ đó ta đưa về bài toán tìm bán kính của mặt cầu ngoại tiếp hình chóp có cạnh bên vuông góc với đáy.

Sử dụng công thức tính nhanh \(R = \sqrt {{r^2} + \dfrac{{{h^2}}}{4}} \)  với \(R\) là bán kính mặt cầu ngoại tiếp hình chóp, \(r\) là bán kính đường tròn ngoại tiếp đáy hình chóp, \(h\) là chiều cao hình chóp

Sử dụng công thức tính diện tích mặt cầu \(S = 4\pi {R^2}\)

Lời giải chi tiết:

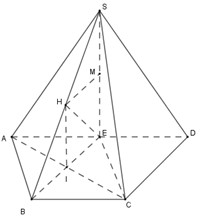
Gọi \(E\) là trung điểm của \(AD\) suy ra \(AE = \dfrac{{AD}}{2} = a = AB = BC\)

Mà \(BC//AD\) và \(BC \bot AD\) nên \(EABC\) là hình vuông cạnh \(a.\)

Lại có \(\left\{ \begin{array}{l}\left( {SAD} \right) \bot \left( {ABCD} \right)\\\left( {SAD} \right) \cap \left( {ABCD} \right) = AD\end{array} \right.\)  mà \(SE \bot AD\) (do tam giác \(SAD\) đều có \(SE\) là trung tuyến)

Suy ra \(SE \bot \left( {ABCD} \right) \Rightarrow SE \bot \left( {EABC} \right)\)

Nhận thấy \(EABC\) là hình vuông nên đường tròn ngoại tiếp \(EABC\) cũng là đường tròn ngoại tiếp tam giác \(ABC\)

Hay mặt cầu ngoại tiếp hình chóp \(S.ABC\) cũng là mặt cầu ngoại tiếp hình chóp \(S.EABC\).

Mà hình chóp \(S.EABC\) có cạnh bên \(SE \bot \left( {EABC} \right)\) và đáy \(EABC\) là hình vuông cạnh \(a.\)  Gọi \(I\) là tâm hình vuông \(EABC\)

Suy ra bán kính mặt cầu ngoại tiếp chóp \(S.EABC\) là \(R = \sqrt {I{E^2} + \dfrac{{S{E^2}}}{4}} \)

Ta có \(BE = \sqrt {A{E^2} + A{B^2}}  = a\sqrt 2  \Rightarrow IE = \dfrac{{a\sqrt 2 }}{2}\)

Tam giác \(SAD\) đều cạnh \(2a\) có \(SE\) là trung tuyến nên \(SE = \dfrac{{2a\sqrt 3 }}{2} = a\sqrt 3 \)

Suy ra \(R = \sqrt {I{E^2} + \dfrac{{S{E^2}}}{4}}  = \sqrt {\dfrac{{2{a^2}}}{4} + \dfrac{{3{a^2}}}{4}}  = \dfrac{{a\sqrt 5 }}{2}\)

Diện tích mặt cầu là \(S = 4\pi {R^2} = 4\pi .\dfrac{{5{a^2}}}{4} = 5\pi {a^2}\)

Chọn B.