Phương pháp giải:

+) Gọi \(G\) là tâm đường tròn ngoại tiếp tam giác \(ABC\). Chứng minh \(G\) là tâm mặt cầu ngoại tiếp chóp \(S.ABC\).

+) Trung tuyến của tam giác đều cạnh a là \(\dfrac{{a\sqrt 3 }}{2}\).

Lời giải chi tiết:

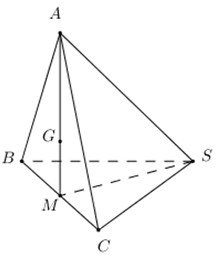
Gọi \(G\) là tâm đường tròn ngoại tiếp tam giác \(ABC \Rightarrow GA = GB = GC\,\,\left( 1 \right)\).

Gọi \(M\) là trung điểm của \(BC\) ta có:

\(\left\{ \begin{array}{l}\left( {ABC} \right) \cap \left( {SBC} \right) = BC\\\left( {ABC} \right) \bot \left( {SBC} \right)\\AM \subset \left( {ABC} \right),\,\,AM \bot BC\end{array} \right. \Rightarrow AM \bot \left( {SBC} \right)\) .

Lại có \(\Delta SBC\) vuông tại \(S\,\,\left( {gt} \right) \Rightarrow M\) là tâm đường tròn ngoại tiếp tam giác \(SBC\).

\( \Rightarrow SM\) là trục của tam giác \(SBC\). Mà \(G \in AM \Rightarrow GS = GB = GC\,\,\left( 2 \right)\).

Từ (1) và (2) \( \Rightarrow GA = GB = GC = GS \Rightarrow G\) là tâm mặt cầu ngoại tiếp chóp \(S.ABC\).

Tam giác \(ABC\) đều cạnh \(a \Rightarrow AM = \dfrac{{a\sqrt 3 }}{2} \Rightarrow GA = \dfrac{2}{3}AM = \dfrac{{a\sqrt 3 }}{3}\).

Chọn C.