Câu hỏi
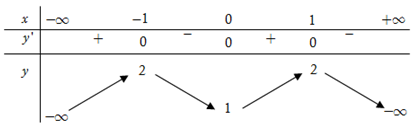
Cho hàm số \(y = a{x^4} + b{x^2} + c{\rm{ }}\left( {a \ne 0} \right)\) có bảng biến thiên dưới đây:
Tính \(P = a - 2b + 3c.\)
- A \(P = 3.\)
- B \(P = 6.\)
- C \(P = - 2.\)
- D \(P = 2.\)
Phương pháp giải:
Dựa vào BBT để xác định các điểm mà đồ thị hàm số đi qua và các điểm cực trị của hàm số rồi từ đó xác định các giá trị a, b, c.
Lời giải chi tiết:
Ta có: \(y = a{x^4} + b{x^2} + c{\rm{ }}\left( {a \ne 0} \right) \Rightarrow y' = 4a{x^3} + 2bx\)
Dựa vào bảng biến thiên, ta thầy đồ thị hàm số đi qua các điểm \(\left( { - 1;\;2} \right),\;\left( {0;\;1} \right),\;\left( {1;\;2} \right)\) và các các điểm này là các điểm cực trị của hàm số.
\( \Rightarrow \left\{ \begin{array}{l}y\left( 0 \right) = 1\\y\left( 1 \right) = 2\\y'\left( 1 \right) = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = 1\\a + b + c = 2\\4a + 2b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = 1\\a + b = 1\\2a + b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 1\\b = 2\\c = 1\end{array} \right.\)
Khi đó: \(P = a - 2b + 3c = - 1 - 2.2 + 3.1 = - 2\).
Chọn C.