Câu hỏi
Đường cong trong hình vẽ bên là đồ thị của hàm số nào sau đây ?
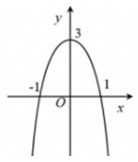
- A \(y = - {x^4} - 2{x^2} + 3\)
- B \(y = {x^4} + 2{x^2} - 3\)
- C \(y = - {x^4} + 2{x^2} + 3\)
- D \(y = - {x^2} + 3\)
Phương pháp giải:
Dựa vào \(\mathop {\lim }\limits_{x \to + \infty } y\) và các giao điểm của đồ thị hàm số với trục hoành.
Lời giải chi tiết:
Dựa vào đồ thị hàm số ta thấy \(\mathop {\lim }\limits_{x \to + \infty } y = - \infty \Rightarrow \) Loại đáp án B.
Đồ thị hàm số cắt trục hoành tại 2 điểm phân biệt có hoành độ \(1\) và \( - 1\) nên chọn đáp án A vì :
Phương trình hoành độ giao điểm \( - {x^4} - 2{x^2} + 3 = 0 \Leftrightarrow \left[ \begin{array}{l}{x^2} = 1\\{x^2} = - 3\,\,\left( {vo\,\,nghiem} \right)\end{array} \right. \Leftrightarrow x = \pm 1\).
Chọn A.







