Câu hỏi
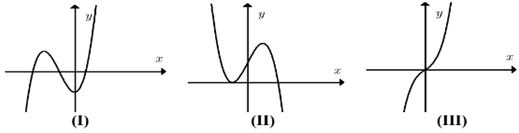
Cho các dạng đồ thị (I), (II), (III) như hình dưới đây:
Đồ thị hàm số \(y = {x^3} + b{x^2} - x + d{\rm{ }}\left( {b,d \in \mathbb{R}} \right)\) có thể là dạng nào trong các dạng trên?
- A (III)
- B (I) và (III)
- C (I) và (II)
- D (I)
Phương pháp giải:
Nhận biết đồ thị hàm số bậc ba.
Lời giải chi tiết:
Ta có: \(y = {x^3} + b{x^2} - x + d \Rightarrow y' = 3{x^2} + 2bx - 1\)
Do \(3.\left( { - 1} \right) < 0 \Rightarrow \)Phương trình \(y' = 0\) luôn có 2 nghiệm phân biệt trái dấu
\( \Rightarrow \)Hàm số đã cho có 2 cực trị với mọi m.
\( \Rightarrow \)Đồ thị hàm số không thể là hình (III)
Mặt khác \(a = 1 > 0 \Rightarrow \) Đồ thị hàm số không thể là hình (II)
Đồ thị hàm số \(y = {x^3} + b{x^2} - x + d{\rm{ }}\left( {b,d \in \mathbb{R}} \right)\) có thể là dạng (I)
Chọn D.