Câu hỏi
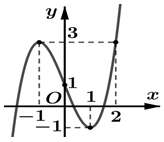
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ dưới. Xét hàm số \(g\left( x \right) = f\left( {2{x^3} + x - 1} \right) + m.\) Tìm \(m\) để \(\mathop {\max }\limits_{\left[ {0;1} \right]} g\left( x \right) = - 10.\)
- A \(m = - 13.\)
- B \(m = 5.\)
- C \(m = 3.\)
- D \(m = - 1.\)
Phương pháp giải:
Khảo sát hàm số \(g\left( x \right)\) trên đoạn \(\left[ {0;1} \right]\), tìm \(\mathop {\max }\limits_{\left[ {0;1} \right]} g\left( x \right)\), từ đó suy ra m.
Lời giải chi tiết:
Ta có: \(g\left( x \right) = f\left( {2{x^3} + x - 1} \right) + m \Rightarrow g'\left( x \right) = \left( {6{x^2} + 1} \right).f'\left( {2{x^3} + x - 1} \right)\)
Với \(x \in \left[ {0;1} \right]\) thì \(\left( {2{x^3} + x - 1} \right) \in \left[ { - 1;\;2} \right]\).
Quan sát đồ thị hàm số \(y = f\left( x \right)\), ta thấy hàm số \(y = f\left( x \right)\) nghịch biến trên đoạn \(\left[ { - 1;1} \right]\)
\( \Rightarrow f'\left( x \right) \le 0,\,\,x \in \left[ { - 1;\;1} \right]\)
\( \Rightarrow f'\left( {2{x^3} + x - 1} \right) \le 0,\,\,\forall x \in \left[ {0;1} \right] \Rightarrow g'\left( x \right) \le 0,\,\,\forall x \in \left[ { - 1;\;2} \right]\) (do \(6{x^2} + 1 > 0,\forall x\))
\( \Rightarrow g\left( x \right)\) nghịch biến trên \(\left[ {0;1} \right] \Rightarrow \)\(\mathop {\max }\limits_{\left[ {0;1} \right]} g\left( x \right) = g\left( 0 \right) = f\left( { - 1} \right) + m = 3 + m\)
Theo đề bài, ta có: \(3 + m = - 10 \Leftrightarrow m = - 13\).
Chọn A.