Phương pháp giải:

Dựng hình lăng trụ \(AEF.BCD\) và tính thể tích tứ diện \(ABCD\) thông qua thể tích hình chóp \(A.CDFE\).

Lời giải chi tiết:

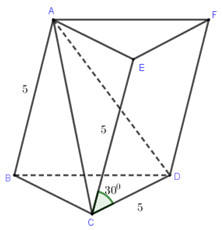
Dựng hình lăng trụ \(AEF.BCD\).

Khi đó, \({V_{ABCD}} = \dfrac{1}{3}{V_{AEF.BCD}} \Rightarrow {V_{A.CDFE}} = \dfrac{2}{3}{V_{AEF.BCD}} \Rightarrow {V_{ABCD}} = \dfrac{1}{2}{V_{A.CDFE}}\)

Ta có: \(d\left( {AB,CD} \right) = d\left( {AB,\left( {CDFE} \right)} \right) = d\left( {A,\left( {CDFE} \right)} \right)\)

\( \Rightarrow d\left( {A,\left( {CDFE} \right)} \right) = 12\)

Lại có \(CE = AB = CD = 5\) và \(\widehat {\left( {AB,CD} \right)} = \widehat {\left( {CE,CD} \right)} = \widehat {ECD} = {30^0}\)

Nên \({S_{CDFE}} = CE.CD.\sin {30^0} = 5.5.\dfrac{1}{2} = \dfrac{{25}}{2}\)

Do đó \({V_{A.CDFE}} = \dfrac{1}{3}d\left( {A,\left( {CDFE} \right)} \right).{S_{CDFE}} = \dfrac{1}{3}.12.\dfrac{{25}}{2} = 50\)

Vậy \({V_{ABCD}} = \dfrac{1}{2}{V_{A.CDFE}} = \dfrac{1}{2}.50 = 25\).

Chọn C.