Câu hỏi
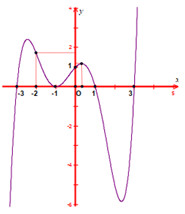
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của \(m\) để phương trình \(\left| {f\left( {\left| {x - 2} \right|} \right) + 1} \right| - m = 0\) có \(8\) nghiệm phân biệt trong khoảng \(\left( { - 5;5} \right)?\)
- A 0
- B 2
- C 1
- D 3
Phương pháp giải:
Sử dụng phép tính tiến đồ thị: với \(a;b > 0\) thì đồ thị hàm số \(y = f\left( {x - a} \right)\) có được do ta tịnh tiến đồ thị hàm số \(y = f\left( x \right)\) sang phải \(a\) đơn vị (hay tịnh tiến đồ thị \(y = f\left( x \right)\) theo vecto \(\overrightarrow u \left( {a;0} \right)\) ) và đồ thị hàm số \(y = f\left( x \right) + b\) có được do ta tịnh tiến đồ thị hàm số \(y = f\left( x \right)\) lên trên \(b\) đơn vị (hay tịnh tiến đồ thị \(y = f\left( x \right)\) theo vecto \(\overrightarrow v \left( {0;b} \right)\) )
Sử dụng cách vẽ đồ thị hàm số \(y = \left| {f\left( {\left| x \right|} \right)} \right|\) từ đồ thị hàm số \(f\left( x \right).\)
+ Vẽ đồ thị hàm số \(y = f\left( x \right)\)
+ Bỏ đi phần đồ thị của \(f\left( x \right)\) nằm bên trái \(Oy,\) lấy đối xứng phần đồ thị phía bên phải \(Oy\) qua \(Oy,\) ta được đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\)
+ Tiếp tục giữ nguyên phần đồ thị phía trên \(Ox,\) lấy đối xứng phần đồ thị phía dưới \(Ox\) qua \(Ox\) rồi gạch bỏ phần đồ thị phía dưới \(Ox\) ta được đồ thị hàm số \(y = \left| {f\left( {\left| x \right|} \right)} \right|\)
Sử dụng sự tương giao của hai đồ thị để biện luận số nghiệm của phương trình đã cho.
Lời giải chi tiết:
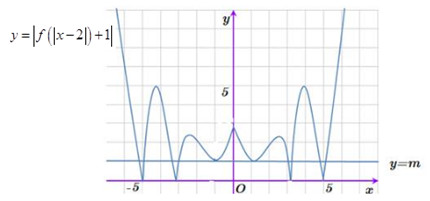
Số nghiệm của phương trình \(\left| {f\left( {\left| {x - 2} \right|} \right) + 1} \right| - m = 0 \Leftrightarrow \left| {f\left( {\left| {x - 2} \right|} \right) + 1} \right| = m\) chính là giao điểm của đồ thị hàm số \(y = \left| {f\left( {\left| {x - 2} \right|} \right) + 1} \right|\) và đường thẳng \(y = m.\)
Ta vẽ đồ thị hàm số \(y = \left| {f\left( {\left| {x - 2} \right|} \right) + 1} \right|\) lần lượt theo các bước như sau:
+ Tịnh tiến đồ thị hàm số \(y = f\left( x \right)\) sang phải \(2\) đơn vị ta được đồ thị hàm số \(y = f\left( {x - 2} \right)\)
+ Bỏ đi phần đồ thị của \(f\left( {x - 2} \right)\) nằm bên trái \(Oy,\) lấy đối xứng phần đồ thị phía bên phải \(Oy\) qua \(Oy,\) ta được đồ thị hàm số \(y = f\left( {\left| {x - 2} \right|} \right)\)
+ Tịnh tiến đồ thị hàm số \(y = f\left( {\left| {x - 2} \right|} \right)\) lên trên \(1\) đơn vị ta được đồ thị hàm số \(y = f\left( {\left| {x - 2} \right|} \right) + 1\)
+ Tiếp tục giữ nguyên phần đồ thị phía trên \(Ox,\) lấy đối xứng phần đồ thị phía dưới \(Ox\) qua \(Ox\) rồi gạch bỏ phần đồ thị phía dưới \(Ox\) ta được đồ thị hàm số \(y = \left| {f\left( {\left| {x - 2} \right|} \right) + 1} \right|\) như hình vẽ trên.
Như vậy đường thẳng \(y = m\) cắt đồ thị hàm số \(y = \left| {f\left( {\left| {x - 2} \right|} \right) + 1} \right|\) tại \(8\) điểm phân biệt khi \(m = 1.\)
Do đó có một số nguyên \(m\) thỏa mãn đề bài.
Chọn C.







