Phương pháp giải:

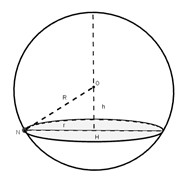
Cho khối cầu \(\left( {O;R} \right)\) ; mặt phẳng \(\left( P \right)\) thỏa mãn \(d\left( {O;\left( P \right)} \right) = h < R\)

Khi đó, mặt phẳng cắt khối cầu theo giao tuyến là đường tròn \(\left( {H;r} \right)\)

Mối liên hệ \({R^2} = {h^2} + {r^2}\)

Tính diện tích hình tròn bán kính \(r\) theo công thức \(S = \pi {r^2}\) .

Lời giải chi tiết:

Mặt phẳng \(\left( P \right)\) cắt mặt cầu theo giao tuyến là đường tròn tâm \(H\) bán  kính \(r\)

Theo giả thiết ta có \(ON = 5;OH = 4 \Rightarrow H{N^2} = O{N^2} - O{H^2} = {5^2} - {4^2} = {3^2}\) \( \Rightarrow HN = 3 \Rightarrow r = 3\)

Diện tích thiết diện là \(S = \pi {r^2} = \pi {.3^2} = 9\pi \)

Chọn  C.