Phương pháp giải:

- Tính thể tích \({V_{S.ABC}}\).

- Tính thể tích \({V_{S.AMN}}\) theo công thức tỉ lệ thể tích.

- Tính thể tích \(V = {V_{A.BCNM}}\) và suy ra kết luận.

Lời giải chi tiết:

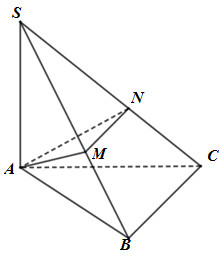
Xét tam giác \(SAB\) và \(SAC\) là các tam giác vuông tại \(A\) có hai cạnh góc vuông là \(a\) và \(2a\) nên \(SB = SC = \sqrt {{a^2} + {{\left( {2a} \right)}^2}}  = a\sqrt 5 \)

Tam giác SAB vuông tại A có đường cao AM

Khi đó \(S{A^2} = SM.SB \Leftrightarrow \dfrac{{S{A^2}}}{{S{B^2}}} = \dfrac{{SM}}{{SB}} \Rightarrow \dfrac{{SM}}{{SB}} = \dfrac{4}{5}\)

Tương tự \(\dfrac{{SN}}{{SC}} = \dfrac{4}{5}\)

Lại có \({V_{S.ABC}} = \dfrac{1}{3}SA.{S_{ABC}} = \dfrac{1}{3}.2{\rm{a}}{\rm{.}}\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 3 }}{6}\)

Mặt khác \(\dfrac{{{V_{S.AMN}}}}{{{V_{S.ABC}}}} = \dfrac{{SA}}{{SA}}.\dfrac{{SM}}{{SB}}.\dfrac{{SN}}{{SC}} = \dfrac{{16}}{{25}} \Rightarrow {V_{A.BCNM}} = \dfrac{9}{{25}}{V_{S.ABC}}\)

Do đó \(V = {V_{A.BCNM}} = \dfrac{9}{{25}}.\dfrac{{{a^3}\sqrt 3 }}{6} = \dfrac{{3{{\rm{a}}^3}\sqrt 3 }}{{50}} \Rightarrow \dfrac{{50V\sqrt 3 }}{{{a^3}}} = 9\).

Chọn C.