Phương pháp giải:

Xác định mặt phẳng \(\left( {ABMN} \right)\) .

Sử dụng tỉ số thể tích: Cho chóp tam giác \(S.ABC\)  có \(M \in SA;\,N \in SB;P \in SC\) .

Khi đó ta có \(\dfrac{{{V_{S.MNP}}}}{{{V_{S.ABC}}}} = \dfrac{{SM}}{{SA}}.\dfrac{{SN}}{{SB}}.\dfrac{{SP}}{{SC}}\)

Từ đó tính được tỉ số  \(\dfrac{{V{ _{S.AMN}}}}{{{V_{S.ACD}}}};\,\dfrac{{{V_{S.AMB}}}}{{{V_{S.ACB}}}} \Rightarrow \dfrac{{{V_{S.ABMN}}}}{{{V_{S.ABCD}}}}\) kết hợp điều kiện đề bài ta tìm được \(x.\)

Lời giải chi tiết:

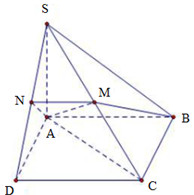
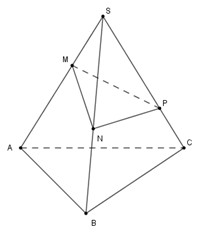
Lấy \(M \in SC\), qua \(M\) kẻ đường thẳng song song với \(AB\) cắt \(SD\) tại \(N\) ta được mặt phẳng \(\left( {ABMN} \right)\) thỏa mãn điều kiện.

Vì \(MN//AB \Rightarrow MN//CD\) nên theo định lý Ta-lét ta có  \(\dfrac{{SM}}{{SC}} = \dfrac{{SN}}{{SD}} = x\)

Vì \(ABCD\)  là hình bình hành nên \({V_{S.ACB}} = {V_{S.ACD}} = \dfrac{1}{2}{V_{S.ABCD}} = \dfrac{1}{2}V\)

Và \(\dfrac{{{V_{S.AMN}}}}{{{V_{S.ACD}}}} = \dfrac{{SA}}{{SA}}.\dfrac{{SM}}{{SC}}.\dfrac{{SN}}{{SD}} = {x^2};\,\,\dfrac{{{V_{S.AMB}}}}{{{V_{S.ACB}}}} = \dfrac{{SA}}{{SA}}.\dfrac{{SM}}{{SC}}.\dfrac{{SB}}{{SB}} = x\)

Suy ra \(\dfrac{{V{ & _{S.AMN}}}}{{{V_{S.ACD}}}} = 2\dfrac{{{V_{S.AMN}}}}{{{V_{S.ABCD}}}} = {x^2} \Rightarrow \dfrac{{{V_{S.AMN}}}}{{{V_{S.ABCD}}}} = \dfrac{{{x^2}}}{2};\,\)

\(\dfrac{{{V_{S.AMB}}}}{{{V_{S.ACB}}}} = 2.\dfrac{{{V_{S.AMB}}}}{{{V_{S.ABCD}}}} = x \Rightarrow \dfrac{{{V_{S.AMB}}}}{{{V_{S.ABCD}}}} = \dfrac{x}{2}\)

Lại có \({V_{S.AMN}} + {V_{S.AMB}} = {V_{S.ABMN}}\)  nên \(\dfrac{{V{ & _{S.AMN}}}}{{{V_{S.ABCD}}}} + \dfrac{{{V_{S.AMB}}}}{{{V_{S.ABCB}}}} = \dfrac{{{V_{S.ABMN}}}}{{{V_{S.ABCD}}}} = \dfrac{{{x^2} + x}}{2}\)

Theo giả thiết ta có  \(\dfrac{{{V_{S.ABMN}}}}{{{V_{S.ABCD}}}} = \dfrac{{11}}{{200}}\)

\( \Rightarrow \dfrac{{{x^2} + x}}{2} = \dfrac{{11}}{{200}} \Leftrightarrow \left\{ \begin{array}{l}0 < x < 1\\100{x^2} + 100x - 11 = 0\end{array} \right. \Leftrightarrow x = 0,1\)

Chọn: A