Câu hỏi
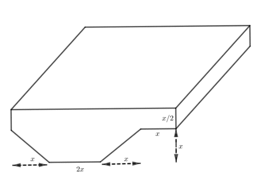
Người ta muốn xây dựng một bể bơi (hình vẽ bên dưới) có thể tích là \(V = \dfrac{{968}}{{4 + 2\sqrt 2 }}\) (\({m^3}\)). Khi đó giá trị thực của \(x\) để diện tích xung quanh của bể bơi là nhỏ nhất thuộc khoảng nào sau đây?
- A \(\left( {0;3} \right)\)
- B \(\left( {3;5} \right)\)
- C \(\left( {5;6} \right)\)
- D \(\left( {2;4} \right)\)
Phương pháp giải:
Nhận xét rằng bể bơi có dạng khối lăng trụ có đáy là hình chữ nhật bị cắt đi một tam giác vuông cân và một hình thang vuông
Từ đó tính được diện tích xung quanh của bể bơi chính là diện tích toàn phần trừ đi diện tích hình chữ nhật là mặt bể bơi
Sau đó dùng bất đẳng thức Cô-si cho ba số \(a,b,c\) không âm \(a + b + c \ge 3\sqrt[3]{{abc}}\) để tìm giá trị nhỏ nhất của diện tích xung quanh.
Lời giải chi tiết:
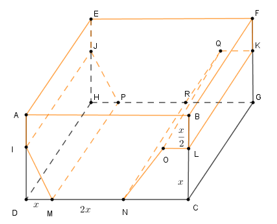
Gọi chiều cao của khối lăng trụ bể bơi là \(h\,\,\left( {h > 0} \right)\) ta có
\(V = S.h = \left( {5x.\dfrac{{3x}}{2} - \dfrac{{x.x}}{2} - \dfrac{{2x + x}}{2}} \right).h = \dfrac{{11{x^2}}}{2} \Leftrightarrow h = \dfrac{{2V}}{{11{x^2}}}\)
Diện tích xung quanh của bể bơi là
\(\begin{array}{l}{S_{xq}} = {S_{AIJE}} + {S_{IMPJ}} + {S_{MNPR}} + {S_{NOQR}} + {S_{OLKQ}} + {S_{BLKF}} + 2.{S_{MNIABLON}}\\\,\,\,\,\,\,\,\, = \dfrac{x}{2}.h + x\sqrt 2 .h + 2x.h + x\sqrt 2 .h + x.h + \dfrac{x}{2}.h + 2.\dfrac{{11{x^2}}}{2}\\\,\,\,\,\,\,\,\, = \left( {4 + 2\sqrt 2 } \right)x.h + 2.\dfrac{{11{x^2}}}{2} = \left( {4 + 2\sqrt 2 } \right)x.\dfrac{{2V}}{{11{x^2}}} + 11{x^2}\\\,\,\,\,\,\,\,\, = \left( {4 + 2\sqrt 2 } \right).\dfrac{{2V}}{{11x}} + 11{x^2}\end{array}\)
Áp dụng bất đẳng thức Cô-si cho ba số ta có
\({S_{xq}} = \dfrac{{\left( {4 + 2\sqrt 2 } \right).V}}{{11x}} + \dfrac{{\left( {4 + 2\sqrt 2 } \right).V}}{{11x}} + 11{x^2} \ge 3\sqrt[3]{{\dfrac{{{{\left( {4 + 2\sqrt 2 } \right)}^2}.{V^2}}}{{11}}}}\)
Vậy \(Min\,{S_{xq}} = 3\sqrt[3]{{\dfrac{{{{\left( {4 + 2\sqrt 2 } \right)}^2}.{V^2}}}{{11}}}}\) khi và chỉ khi
\(\dfrac{{\left( {4 + 2\sqrt 2 } \right)V}}{{11x}} = 11{x^2} \Rightarrow {x^3} = \dfrac{{\left( {4 + 2\sqrt 2 } \right)V}}{{121}} = 8 \Rightarrow x = 2\)
Chọn A.