Câu hỏi
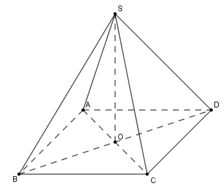
Cho hình chóp tứ giác đều \(S.ABCD\) có cạnh đáy bằng \(2a\) cạnh bên bằng \(3a\). Tính thể tích \(V\) của khối chóp đã cho?
- A \(V = \dfrac{{4\sqrt 7 {a^3}}}{9}\)
- B \(V = 4\sqrt 7 {a^3}\)
- C \(V = \dfrac{{4\sqrt 7 {a^3}}}{3}\)
- D \(V = \dfrac{{4{a^3}}}{3}\)
Phương pháp giải:
Sử dụng công thức tính thể tích khối chóp \(V = \dfrac{1}{3}S.h\) với \(h\) là chiều cao hình chóp, \(S\) là diện tích đáy.
Lời giải chi tiết:
Ta có chóp tứ giác đều \(S.ABCD\) có \(SA = SB = SC = SD = 3a;\,AB = AD = BC = DC = 2a\), chiều cao \(SO\) (với \(O\) là tâm \(ABCD\) )
Ta có \(BD = \sqrt {B{C^2} + D{C^2}} = 2a\sqrt 2 \Rightarrow BO = \dfrac{{BD}}{2} = a\sqrt 2 \)
Tam giác \(SOB\) vuông tại \(O \Rightarrow SO = \sqrt {S{B^2} - B{O^2}} = \sqrt {9{a^2} - {{\left( {a\sqrt 2 } \right)}^2}} = a\sqrt 7 \)
Diện tích đáy \({S_{ABCD}} = B{C^2} = 4{a^2}\)
Thể tích \({V_{S.ABC}} = \dfrac{1}{3}.{S_{ABCD}}.SO = \dfrac{1}{3}.4{a^2}.a\sqrt 7 = \dfrac{{4\sqrt 7 {a^3}}}{3}\)
Chọn C.