Câu hỏi
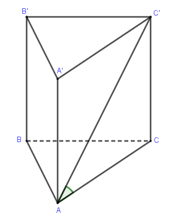
Cho khối lăng trụ đứng tam giác \(ABC.A'B'C'\) có đáy là một tam giác vuông cân tại \(A\), \(AC = AB = 2a\), góc giữa \(AC'\) và mặt phẳng \(\left( {ABC} \right)\) bằng \(30^\circ \). Thể tích khối lăng trụ \(ABC.A'B'C'\) là
- A \(\dfrac{{4a\sqrt 3 }}{3}\)
- B \(\dfrac{{2{a^3}\sqrt 3 }}{3}\)
- C \(\dfrac{{4{a^3}\sqrt 3 }}{3}\)
- D \(\dfrac{{4{a^2}\sqrt 3 }}{3}\)
Phương pháp giải:
- Xác định góc giữa đường thẳng \(AC'\) với \(\left( {ABC} \right)\)
- Tính thể tích lăng trụ theo công thức \(V = B.h\)
Lời giải chi tiết:
Vì \(C'C \bot \left( {ABC} \right)\) nên góc giữa \(C'A\) và \(\left( {ABC} \right)\) là \(\widehat {\left( {C'A,CA} \right)} = \widehat {C'AC} = {30^0}\) (vì \(\widehat {C'AC} < {90^0}\)).
Tam giác \(ACC'\) vuông tại \(C\) có \(AC = 2a,\widehat {C'AC} = {30^0}\) nên \(CC' = AC\tan {30^0} = 2a.\dfrac{{\sqrt 3 }}{3} = \dfrac{{2a\sqrt 3 }}{3}\)
Vậy thể tích khối lăng trụ là:
\({V_{ABC.A'B'C'}} = {S_{ABC}}.CC' = \dfrac{1}{2}AB.AC.CC' = \dfrac{1}{2}.2a.2a.\dfrac{{2a\sqrt 3 }}{3} = \dfrac{{4{a^3}\sqrt 3 }}{3}\)
Chọn C.