Câu hỏi
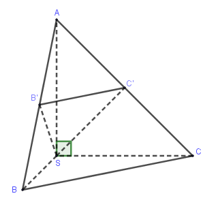
Cho hình chóp \(S.ABC\) có \(SA\), \(SB\), \(SC\) đôi một vuông góc và \(SA = SB = SC = a\). Gọi \(B'\), \(C'\) lần lượt là hình chiếu vuông góc của \(S\) trên \(AB\), \(AC\). Tính thể tích hình chóp \(S.AB'C'\)
- A \(V = \dfrac{{{a^3}}}{{24}}\)
- B \(V = \dfrac{{{a^3}}}{{12}}\)
- C \(V = \dfrac{{{a^3}}}{6}\)
- D \(V = \dfrac{{{a^3}}}{{48}}\)
Phương pháp giải:
Phương pháp:
- Tính tỉ số thể tích \(\dfrac{{{V_{S.AB'C'}}}}{{{V_{S.ABC}}}}\)
- Tính thể tích \({V_{S.ABC}}\) và suy ra kết luận.
Lời giải chi tiết:
Do các tam giác \(ASB,ASC\) vuông cân tại \(S\) nên \(B',C'\) lần lượt là trung điểm của \(AB,AC\).
Ta có: \(\dfrac{{{V_{S.AB'C'}}}}{{{V_{S.ABC}}}} = \dfrac{{{V_{A.SBC}}}}{{{V_{A.SB'C'}}}} = \dfrac{{AB'}}{{AB}}.\dfrac{{AC'}}{{AC}} = \dfrac{1}{2}.\dfrac{1}{2} = \dfrac{1}{4}\)
Lại có: \(S.ABC\) là tứ diện vuông nên \({V_{S.ABC}} = \dfrac{1}{6}SA.SB.SC = \dfrac{1}{6}{a^3}\).
Vậy \({V_{S.AB'C'}} = \dfrac{1}{4}.{V_{S.ABC}} = \dfrac{1}{4}.\dfrac{1}{6}{a^3} = \dfrac{{{a^3}}}{{24}}\)
Chọn A.
Câu hỏi trước
