Câu hỏi
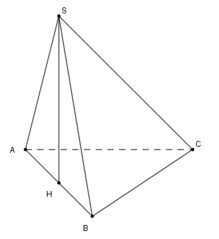
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(2a\), tam giác \(SAB\) là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Tính thể tích khối chóp \(S.ABC\).
- A \(V = {a^3}\)
- B \(V = 3{a^3}\)
- C \(V = \dfrac{{3{a^3}}}{2}\)
- D \(V = \dfrac{{{a^3}}}{2}\)
Phương pháp giải:
+ Sử dụng kiến thức \(\left\{ \begin{array}{l}\left( P \right) \bot \left( Q \right)\\\left( P \right) \cap \left( Q \right) = a\\d \bot a;\,d \subset \left( P \right)\end{array} \right. \Rightarrow d \bot \left( Q \right)\) để tìm ra chiều cao của hình chóp
+ Sử dụng công thức tính diện tích tam giác đều cạnh \(x\) là \(S = \dfrac{{{x^2}\sqrt 3 }}{4}\), đường trung tuyến tam giác đều cạnh \(x\) là \(\dfrac{{x\sqrt 3 }}{2}\)
+ Sử dụng công thức tính thể tích khối chóp \(V = \dfrac{1}{3}S.h\) với \(h\) là chiều cao hình chóp, \(S\) là diện tích đáy.
Lời giải chi tiết:
Gọi \(H\) là trung điểm của \(AB\) khi đó \(SH \bot AB\) (vì tam giác \(SAB\) đều có đường trung tuyến trùng với đường cao)
Ta có \(\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {ABC} \right)\\\left( {SAB} \right) \cap \left( {ABC} \right) = AB\\SH \bot AB;\,SH \subset \left( {SAB} \right)\end{array} \right.\) nên \(SH \bot \left( {ABC} \right)\) tại \(H.\)
Vì \(ABC\) là tam giác đều cạnh \(2a\) nên \(AB = 2a\) và \({S_{ABC}} = \dfrac{{{{\left( {2a} \right)}^2}\sqrt 3 }}{4} = {a^2}\sqrt 3 \)
Tam giác \(SAB\) là tam giác đều cạnh \(2a\) (vì \(AB = 2a\) ) có \(SH\) là đường trung tuyến nên \(SH = \dfrac{{2a\sqrt 3 }}{2} = a\sqrt 3 \)
Thể tích khối chóp \({V_{S.ABC}} = \dfrac{1}{3}{S_{ABC}}.SH = \dfrac{1}{3}.{a^2}\sqrt 3 .\dfrac{{a\sqrt 3 }}{2} = {a^3}\) (đvtt)
Chọn A.