Câu hỏi
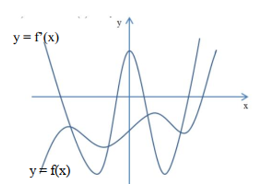
Cho hàm số \(f\left( x \right)\) có đồ thị của \(f\left( x \right);\,f'\left( x \right)\) như hình vẽ. Mệnh đề nào sau đây đúng?
- A \(f'\left( { - 1} \right) \ge f''\left( 1 \right)\)
- B \(f'\left( { - 1} \right) > f''\left( 1 \right)\)
- C \(f'\left( { - 1} \right) < f''\left( 1 \right)\)
- D \(f'\left( { - 1} \right) = f''\left( 1 \right)\)
Phương pháp giải:
Từ hình vẽ ta xác định được đồ thị hàm số \(y = f\left( x \right)\) và \(y = f'\left( x \right)\)
Từ đồ thị hàm số suy ra hàm số đạt cực trị tại \({x_0} \Rightarrow f'\left( {{x_0}} \right) = 0\) , hàm số đạt cực đại tại \({x_0} \Rightarrow f''\left( {{x_0}} \right) < 0\) để so sánh.
Lời giải chi tiết:
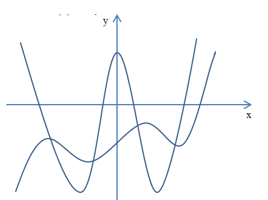
Từ hình vẽ ta xác định được đồ thị hàm số \(y = f\left( x \right)\) và \(y = f'\left( x \right)\) như hình vẽ ( do đồ thị \(y = f\left( x \right)\) có 4 điểm cực trị và đồ thị \(y = f'\left( x \right)\) cắt trục hoành tại 4 điểm phân biệt)
Từ đồ thị ta thấy hàm số \(y = f\left( x \right)\) đạt cực tiểu tại \(x = - 1 \Rightarrow f'\left( { - 1} \right) = 0\)
Lại thấy hàm số \(y = f\left( x \right)\) đạt cực đại tại \(x = 1 \Rightarrow f'\left( 1 \right) = 0;\,f''\left( 1 \right) < 0\)
Từ đó ta có \(f'\left( { - 1} \right) > f''\left( 1 \right)\) .
Chọn B.