Câu hỏi
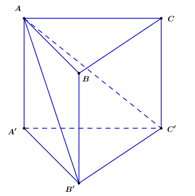
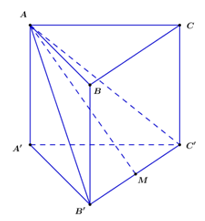
Cho khối lăng trụ đều \(ABC.A'B'C'\) có cạnh đáy bằng \(a.\) Khoảng cách từ điểm \(A'\) đến mặt phẳng \(\left( {AB'C'} \right)\) bằng \(\dfrac{{2a\sqrt 3 }}{{\sqrt {19} }}.\) Thể tích khối lăng trụ đã cho là:
- A \(\dfrac{{{a^3}\sqrt 3 }}{6}\)
- B \(\dfrac{{{a^3}\sqrt 3 }}{2}\)
- C \(\dfrac{{{a^3}\sqrt 3 }}{4}\)
- D \(\dfrac{{3{a^3}}}{2}\)
Phương pháp giải:
Công thức tính thể tích khối lăng trụ có chiều cao \(h\) và diện tích đáy \(S\) là: \(V = Sh.\)
Lời giải chi tiết:
Gọi chiều cao của khối lăng trụ đều \(ABC.A'B'C'\) là \(AA' = x.\)
Khi đó ta có: \({V_{ABC.A'B'C'}} = AA'.{S_{ABC}} = x.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^2}x\sqrt 3 }}{4}.\)
Ta có: \({V_{AA'B'C'}} = \dfrac{1}{3}{V_{ABC.A'B'C'}} = \dfrac{1}{3}.\dfrac{{{a^2}x\sqrt 3 }}{4} = \dfrac{{{a^2}x\sqrt 3 }}{{12}}.\)
Gọi \(M\) là trung điểm của \(B'C' \Rightarrow AM \bot B'C'.\)
Áp dụng định lý Pi-ta-go ta có:
\(\begin{array}{l}AB' = AC' = \sqrt {AA{'^2} + A'B{'^2}} = \sqrt {{x^2} + {a^2}} .\\ \Rightarrow AM = \sqrt {AB{'^2} - B'{M^2}} = \sqrt {{x^2} + {a^2} - \dfrac{{{a^2}}}{4}} = \sqrt {{x^2} + \dfrac{{3{a^2}}}{4}} .\\ \Rightarrow {S_{AB'C'}} = \dfrac{1}{2}AM.B'C' = \dfrac{1}{2}.a.\sqrt {{x^2} + \dfrac{{3{a^2}}}{4}} .\end{array}\)
Lại có: \({V_{AA'B'C'}} = \dfrac{1}{3}{S_{AB'C'}}.d\left( {A';\;\left( {AB'C'} \right)} \right)\)
\(\begin{array}{l} \Rightarrow {S_{AB'C'}} = \dfrac{{3{V_{AA'B'C'}}}}{{d\left( {A';\left( {AB'C'} \right)} \right)}} = \dfrac{{3.\dfrac{{{a^2}x\sqrt 3 }}{{12}}}}{{\dfrac{{2a\sqrt 3 }}{{\sqrt {19} }}}} = \dfrac{{ax\sqrt {19} }}{8}.\\ \Rightarrow \dfrac{{ax\sqrt {19} }}{8} = \dfrac{1}{2}a\sqrt {{x^2} + \dfrac{{3{a^2}}}{4}} \Leftrightarrow \dfrac{{ax\sqrt {19} }}{4} = a.\dfrac{{\sqrt {4{x^2} + 3{a^2}} }}{2}\\ \Leftrightarrow x\sqrt {19} = 2\sqrt {4{x^2} + 3{a^2}} \Leftrightarrow 19{x^2} = 16{x^2} + 12{a^2}\\ \Leftrightarrow 3{x^2} = 12{a^2} \Leftrightarrow {x^2} = 4{a^2} \Leftrightarrow x = 2a.\\ \Rightarrow {V_{ABC.A'B'C'}} = \dfrac{{{a^2}.2a\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 3 }}{2}.\end{array}\)
Chọn B.