Câu hỏi
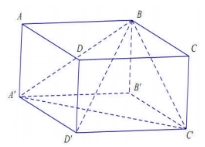
Cho khối hộp chữ nhật ABCD.A’B’C’D’ có \(AB = a,\,\,AD = 2a,\,\,AA' = 3a\). Tính thể tích V của khối tứ diện BA’C’D’.
- A \(V = 2{a^3}\)
- B \(V = 6{a^3}\)
- C \(V = {a^3}\)
- D \(V = 3{a^3}\)
Phương pháp giải:
Sử dụng công thức tính thể tích khối chóp \({V_{chop}} = \dfrac{1}{3}{S_{day}}.h\).
Lời giải chi tiết:
Ta có \({V_{B.A'C'D'}} = \dfrac{1}{3}BB'.{S_{A'C'D'}} = \dfrac{1}{3}BB'.\dfrac{1}{2}{S_{ABCD}} = \dfrac{1}{6}{V_{ABCD.A'B'C'D'}} = \dfrac{1}{6}.a.2a.3a = {a^3}\).
Chọn C.
Câu hỏi trước
