Câu hỏi
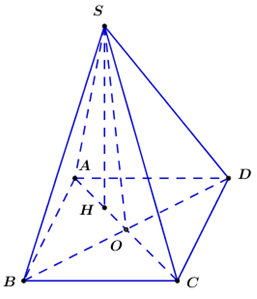
Cho hình chóp \(SABCD\) có \(SC = x\;\;\left( {0 < x < \sqrt 3 } \right),\) các cạnh còn lại đều bằng 1. Thể tích lớn nhất của khối chóp \(SABCD\) bằng:
- A \(\frac{{\sqrt 3 }}{4}\)
- B \(\frac{1}{3}\)
- C \(\frac{1}{4}\)
- D \(\frac{{\sqrt 3 }}{6}\)
Phương pháp giải:
Thể tích của khối chóp có diện tích đáy \(S\) và chiều cao \(h\) là: \(V = Sh.\)
Lời giải chi tiết:
Ta có: \(\Delta SBD = \Delta ABD\;\left( {c - c - c} \right) \Rightarrow AO = SO = OC\)
\( \Rightarrow \Delta SAC\) vuông tại \(S.\) (tam giác có đường trung tuyến từ đỉnh S đến cạnh AC bằng nửa cạnh AC).
\(\begin{array}{l} \Rightarrow AO = \frac{1}{2}AC = \frac{1}{2}\sqrt {S{A^2} + S{C^2}} = \frac{1}{2}\sqrt {1 + {x^2}} .\\ \Rightarrow BO = \sqrt {A{B^2} - A{O^2}} = \sqrt {1 - \frac{{1 + {x^2}}}{4}} = \frac{{\sqrt {3 - {x^2}} }}{2}.\\ \Rightarrow {S_{ABCD}} = \frac{1}{2}AC.BD = \frac{1}{2}.\sqrt {1 + {x^2}} .\sqrt {3 - {x^2}} \\SH = \frac{{SA.SC}}{{\sqrt {S{A^2} + S{C^2}} }} = \frac{x}{{\sqrt {1 + {x^2}} }}\\ \Rightarrow {V_{SABCD}} = \frac{1}{3}SH.{S_{ABCD}} = \frac{1}{3}.\frac{x}{{\sqrt {1 + {x^2}} }}.\frac{1}{2}.\sqrt {1 + {x^2}} .\sqrt {3 - {x^2}} \\ = \frac{1}{6}x\sqrt {3 - {x^2}} = \frac{{\sqrt {{x^2}\left( {3 - {x^2}} \right)} }}{6} \le \frac{1}{2}\frac{{{x^2} + 3 - {x^2}}}{6} = \frac{1}{4}.\\ \Rightarrow Max\;{V_{SABCD}} = \frac{1}{4}.\end{array}\)
Chọn C.