Câu hỏi
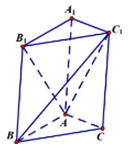
Cho lăng trụ \(ABC.{A_1}{B_1}{C_1}\) có diện tích mặt bên \(AB{B_1}{A_1}\) bằng 6, khoảng cách giữa cạnh \(C{C_1}\) và mặt phẳng \(\left( {AB{B_1}{A_1}} \right)\) bằng 8. Thể tích khối lăng trụ \(ABC.{A_1}{B_1}{C_1}\) bằng:
- A 24
- B 8
- C 16
- D 32
Phương pháp giải:
Thể tích khối lăng trụ có diện tích đáy \(S\) và chiều cao \(h\) là \(V = Sh.\)
Lời giải chi tiết:
Chia khối lăng trụ \(ABC.{A_1}{B_1}{C_1}\) theo mặt phẳng \(\left( {AB{C_1}} \right)\) thành khối chóp \({C_1}.ABC\) và khối chóp tứ giác \({C_1}AB{B_1}{A_1}.\)
Ta có:
\(\begin{array}{l}{V_{{C_1}ABC}} = \frac{1}{3}V \Rightarrow \left\{ \begin{array}{l}{V_{{C_1}AB{B_1}{A_1}}} = \frac{2}{3}V\\{V_{{C_1}AB{B_1}{A_1}}} = \frac{1}{3}d\left( {A;\;\left( {AB{B_1}{A_1}} \right)} \right) = \frac{1}{3}.6.8 = 16\end{array} \right..\\ \Rightarrow V = 16.\frac{3}{2} = 24.\end{array}\)
Chọn A.