Phương pháp giải:

Sử dụng các tính chất của tam giác vuông cân.

Lời giải chi tiết:

Gọi \(B\left( {a;\;2 + \frac{2}{{a - 1}}} \right),\;\;C\left( {c;\;2 + \frac{2}{{c - 1}}} \right)\;\;\left( {a < 1 < c} \right).\)

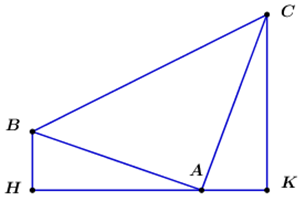
Gọi \(H,\;K\) lần lượt là hình chiếu của \(B,\;C\) trên trục \(Ox \Rightarrow H\left( {a;\;0} \right),\;\;K\left( {c;\;0} \right).\)

\(\Delta ABC\) vuông cân \( \Rightarrow \left\{ \begin{array}{l}AB = AC\\\angle BAC = {90^0}\end{array} \right..\)

Ta có: \(\angle BAC = \angle CAK + \angle ACK = \angle BAH + \angle ABH\)

Mà: \(\angle BAH + \angle CAK = {90^0}\)

\( \Rightarrow \angle BAH = \angle ACK.\)

Xét \(\Delta ABH\) và \(\Delta CAK\) ta có:

\(\begin{array}{l}\angle BAH = \angle ACK\;\;\left( {cmt} \right)\\AC = AB\;\left( {gt} \right)\\ \Rightarrow \Delta ABH = \angle CAK\;\;\left( {ch - gn} \right)\end{array}\)

\( \Rightarrow AH = CK,\;\;HB = AK\) (các cạnh tương ứng bằng nhau)

Ta có: \(AH = \left| {a - 2} \right| = 2 - a;\;\;AK = \left| {c - 2} \right|;\;\;\left( {a < 1} \right).\)

\(\begin{array}{l}BH = \left| {2 + \frac{2}{{a + 1}}} \right|;\;\;CK = \left| {2 + \frac{2}{{c - 1}}} \right| = 2 + \frac{2}{{c - 1}}\;\;\left( {c > 1} \right)\\ \Rightarrow \left\{ \begin{array}{l}AH = CK\\HB = AK\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2 - a = 2 + \frac{2}{{c - 1}}\\\left| {2 + \frac{2}{{a - 1}}} \right| = \left| {c - 2} \right|\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}a = \frac{2}{{1 - c}}\\\left[ \begin{array}{l}2 + \frac{2}{{a - 1}} = c - 2\\2 + \frac{2}{{a - 1}} = 2 - c\end{array} \right.\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{2}{{1 - c}}\\\left[ \begin{array}{l}4 + \frac{2}{{\frac{2}{{1 - c}} - 1}} = c - 2\\c = \frac{2}{{1 - a}} = \frac{2}{{1 - \frac{2}{{1 - c}}}}\end{array} \right.\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b =  - 1\;\;\left( {tm} \right)\\c = 3\;\;\left( {tm} \right)\end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l}B\left( { - 1;\;1} \right)\\C\left( {3;\;3} \right)\end{array} \right. \Rightarrow T = \left( { - 1} \right).1 + 3.3 = 8.\end{array}\)

Chọn  D.