Câu hỏi
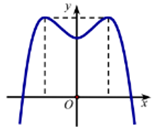
Hàm số \(y = a{x^4} + b{x^2} + c\) có đồ thị hàm số như hình vẽ dưới đây. Mệnh đề nào sau đây đúng?
- A \(a < 0,\;b > 0,\;c > 0\)
- B \(a < 0,\;b > 0,\;c < 0\)
- C \(a > 0,\;b < 0,\;c > 0\)
- D \(a < 0,\;b < 0,\;c > 0\)
Phương pháp giải:
Dựa vào đồ thị hàm số nhận xét số điểm cực trị, các điểm thuộc đồ thị hàm số và các khoảng đồng biến, nghịch biến của hàm số và đưa ra kết luận đúng.
Lời giải chi tiết:
Ta thấy đồ thị hàm số có 2 điểm cực đại và 1 điểm cực tiểu \( \Rightarrow a < 0\) và \(y' = 0\) có 3 nghiệm phân biệt.
Có: \(y' = 4a{x^3} + 2bx = 0 \Leftrightarrow 2x\left( {2a{x^2} + b} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} = - \frac{b}{a}\;\;\left( 1 \right)\end{array} \right.\;\;\)
Phương trình \(y' = 0\) có 3 nghiệm phân biệt \( \Leftrightarrow pt\;\left( 1 \right)\) có 2 nghiệm phân biệt \( \ne 0 \Leftrightarrow - \frac{b}{a} > 0 \Leftrightarrow \frac{b}{a} < 0\) mà \(a < 0 \Rightarrow b > 0.\)
Đồ thị hàm số cắt trục tung tại điểm có tung độ lớn hơn \(0 \Rightarrow c > 0.\)
Chọn A.