Phương pháp giải:

Sử dụng bất đẳng thức Cô-si cho hai số dương và ba số dương.

Khảo sát sự biến thiên của hàm số, tìm giá trị lớn nhất của hàm số.

Lời giải chi tiết:

Áp dụng bất đẳng thức cho hai số dương ta có:

\(P = \frac{{8a + 3b + 4\left( {\sqrt {ab}  + \sqrt {bc}  + \sqrt[3]{{abc}}} \right)}}{{1 + {{\left( {a + b + c} \right)}^2}}} \le \frac{{8a + 3b + 4\left( {\frac{{a + 4b}}{4} + \frac{{b + 4c}}{4} + \frac{{a + 4b + 16c}}{{12}}} \right)}}{{1 + {{\left( {a + b + c} \right)}^2}}} = \frac{{28}}{3}.\frac{{a + b + c}}{{1 + {{\left( {a + b + c} \right)}^2}}}.\)

Đặt \(a + b + c = t,\;\left( {t > 0} \right).\)

Ta có: \(P = \frac{{28}}{3}f\left( t \right) = \frac{{28}}{3}.\frac{t}{{{t^2} + 1}}\;\;\left( {t > 0} \right).\)  

Có: \(f'\left( t \right) = \frac{{1 + {t^2} - 2{t^2}}}{{{{\left( {1 + {t^2}} \right)}^2}}} = \frac{{1 - {t^2}}}{{{{\left( {1 + {t^2}} \right)}^2}}} \Rightarrow f'\left( t \right) = 0 \Leftrightarrow \left[ \begin{array}{l}t = 1\;\;\left( {tm} \right)\\t =  - 1\;\;\left( {ktm} \right)\end{array} \right..\)

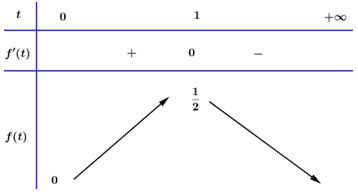
Ta có BBT:

Dựa vào BBT ta có: \(\max f\left( t \right) = \frac{1}{2}\;\;khi\;\;t = 1\)

\( \Rightarrow Max\;P = \frac{{28}}{3}.\frac{1}{2} = \frac{{14}}{3}.\)

Dấu “=” xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}\frac{a}{4} = b\\\frac{b}{4} = c\\a + b + c = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 4b\\b = 4c\\21c = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{{16}}{{21}}\\b = \frac{4}{{21}}\\c = \frac{1}{{21}}\end{array} \right..\)

Chọn  B.