Câu hỏi
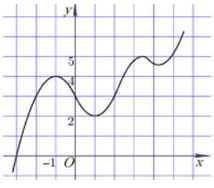
Cho hàm số \(y = f\left( x \right)\) có đồ thị hàm số như hình vẽ dưới. Gọi \(M,\;m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = f\left( {{x^2} - 2x} \right)\) trên đoạn \(\left[ { - \frac{3}{2};\;\frac{7}{2}} \right].\) Tìm khẳng định sai trong các khẳng định sau.
- A \(M + m < 7\)
- B \(Mm > 10\)
- C \(M - m > 3\)
- D \(\frac{M}{m} > 2\)
Phương pháp giải:
Dựa vào đồ thị hàm số đã cho và biến đổi, đặt ẩn phụ để tìm đáp án đúng.
Lời giải chi tiết:
Đặt \(t = {x^2} - 2x,\;\;x \in \left[ { - \frac{3}{2};\;\frac{7}{2}} \right] \Rightarrow \left[ { - 1;\;\frac{{21}}{4}} \right]\)
Từ đồ thị hàm số ta xét hàm số \(y = f\left( t \right),\;\;t \in \left[ { - 1;\;\frac{{21}}{4}} \right]\)
\(\begin{array}{l} \Rightarrow m = \mathop {\min }\limits_{\left[ { - 1;\;\frac{{21}}{4}} \right]} f\left( t \right) = f\left( 2 \right) = 2,\;\;M = \mathop {\max }\limits_{\left[ { - 1;\;\frac{{21}}{4}} \right]} f\left( t \right) > f\left( {\frac{{21}}{4}} \right) = 5.\\ \Rightarrow M + m > 7.\end{array}\)
Chọn A.