Câu hỏi
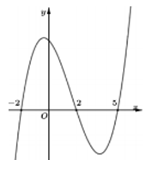
Cho hàm số \(f\left( x \right).\) Đồ thị hàm số \(y = f'\left( x \right)\) như hình vẽ bên. Hàm số \(g\left( x \right) = f\left( {3 - 2x} \right)\) nghịch biến trên khoảng nào trong các khoảng sau?
- A \(\left( {0;\;2} \right)\)
- B \(\left( {1;\;3} \right)\)
- C \(\left( { - \infty ; - 1} \right)\)
- D \(\left( { - 1; + \infty } \right)\)
Phương pháp giải:
Dựa vào đồ thị hàm số \(y = f'\left( x \right)\) suy ra tính đơn điệu của hàm số \(y = f\left( x \right)\) và chọn đáp án đúng.
Lời giải chi tiết:
Ta có: \(\begin{array}{l}f'\left( x \right) > 0 \Leftrightarrow \left[ \begin{array}{l} - 2 < x < 2\\x > 5\end{array} \right.\\g'\left( x \right) = \left[ {f\left( {3 - 2x} \right)} \right]' = - 2f'\left( {3 - 2x} \right)\\ \Rightarrow g'\left( x \right) < 0 \Leftrightarrow f'\left( {3 - 2x} \right) > 0\\ \Leftrightarrow \left[ \begin{array}{l} - 2 < 3 - 2x < 2\\3 - 2x > 5\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\frac{1}{2} < x < \frac{5}{2}\\x < - 1\end{array} \right..\end{array}\)
Chọn C.