Phương pháp giải:

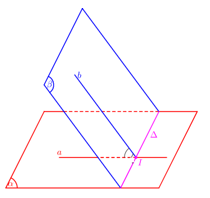
Xác định góc giữa hai mặt phẳng \(\left( \alpha  \right),\,\,\left( \beta  \right)\):

- Tìm giao tuyến \(\Delta \) của \(\left( \alpha  \right),\,\,\left( \beta  \right)\).

- Xác định 1 mặt phẳng \(\left( \gamma  \right) \bot \Delta \).

- Tìm các giao tuyến \(a = \left( \alpha  \right) \cap \left( \gamma  \right),b = \left( \beta  \right) \cap \left( \gamma  \right)\)

- Góc giữa hai mặt phẳng \(\left( \alpha  \right),\,\,\left( \beta  \right)\): \(\left( {\widehat {\left( \alpha  \right);\left( \beta  \right)}} \right) = \left( {\widehat {a;b}} \right)\)

Lời giải chi tiết:

Gọi O là tâm hình vuông ABCD. Hình chóp S.ABCD đều \( \Rightarrow SO \bot \left( {ABCD} \right)\).

Ta có:

\(\begin{array}{l}\left\{ \begin{array}{l}\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\\AB \bot \left( {SPO} \right)\end{array} \right.\\ \Rightarrow \left( {\widehat {\left( {SAB} \right);\left( {ABCD} \right)}} \right) = \left( {\widehat {SP;OP}} \right) = \widehat {SPO} = 45^\circ \end{array}\)

\( \Rightarrow \Delta SOP\) vuông cân tại O

Gọi độ dài cạnh đáy là x \( \Rightarrow OP = \dfrac{x}{2} \Rightarrow SO = OP = \dfrac{x}{2}\)

Khi đó, \({V_{S.ABCD}} = \dfrac{1}{3}.SO.{S_{ABCD}} = \dfrac{1}{3}.\dfrac{x}{2}.{x^2} = \dfrac{{{x^3}}}{6}\)

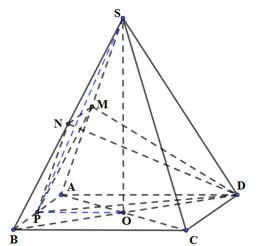
Ta có: \({S_{MNP}} = \dfrac{1}{4}{S_{SAB}}\) (do M, N, P lần lượt là trung điểm của các cạnh SA, SB, AB) \( \Rightarrow {V_{D.MNP}} = \dfrac{1}{4}{V_{S.ABD}}\)

Mà \({V_{S.ABD}} = \dfrac{1}{2}{V_{S.ABCD}} \Rightarrow {V_{D.MNP}} = \dfrac{1}{8}{V_{S.ABCD}} = \dfrac{1}{8}.\dfrac{{{x^3}}}{6} = \dfrac{{{x^3}}}{{48}} \Rightarrow \dfrac{{{x^3}}}{{48}} = \dfrac{{{a^3}}}{6} \Rightarrow x = 2a\).

Chọn: C