Phương pháp giải:

\(\left\{ \begin{array}{l}\left( P \right) \bot \left( Q \right)\\\left( P \right) \cap \left( Q \right) = d\\a \subset \left( P \right)\\a \bot d\end{array} \right.\,\, \Rightarrow a \bot \left( Q \right)\)

Lời giải chi tiết:

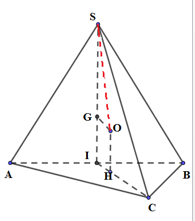
Gọi I là trung điểm của AB, G là trọng tâm tam giác SAB.

Tam giác SAB đều \( \Rightarrow \left\{ \begin{array}{l}SI \bot AB\\SG = \dfrac{2}{3}SI = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\end{array} \right.\)

Ta có:  \(\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {ABC} \right)\\\left( {SAB} \right) \cap \left( {ABC} \right) = AB\\SI \subset \left( {SAB} \right)\\SI \bot AB\end{array} \right.\,\, \Rightarrow SI \bot \left( {ABC} \right)\)

Gọi H là trọng tâm tam giác ABC. Dựng điểm O sao cho \(\left\{ \begin{array}{l}OH//SI\\GO//IC\end{array} \right.\)

Khi đó, O là tâm mặt cầu ngoại tiếp hình chóp S.ABC.

Ta có: SAB, ABC là hai tam giác đều có chung cạnh AB, I là trung điểm của AB \( \Rightarrow SI = CI\)

\(IG = \dfrac{1}{3}SI,\,IH = \dfrac{1}{3}IC \Rightarrow IG = IH \Rightarrow IGOH\) là hình vuông \( \Rightarrow OG = IG = \dfrac{1}{3}SI = \dfrac{1}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{6}\)

Tam giác SGO vuông tại G \( \Rightarrow SO = \sqrt {S{G^2} + G{O^2}}  = \sqrt {\dfrac{{{a^2}}}{3} + \dfrac{{{a^2}}}{{12}}}  = \dfrac{{a\sqrt {15} }}{6} \Rightarrow R = \dfrac{{a\sqrt {15} }}{6}\)

Tính thể tích V của khối cầu ngoại tiếp hình chóp đã cho là: \(V = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}\pi {\left( {\dfrac{{a\sqrt {15} }}{6}} \right)^3} = \dfrac{{5{a^3}\sqrt {15} }}{{54}}\)

Chọn: A