Phương pháp giải:

Thể tích khối nón: \(V = \dfrac{1}{3}\pi {r^2}h\).

Lời giải chi tiết:

Bán kính \(r = \dfrac{{2a\sqrt 3 }}{2} = a\sqrt 3 \)

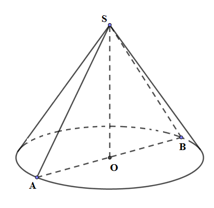
Hình nón có góc ở đỉnh là \(120^\circ  \Rightarrow \widehat {ASB} = 120^\circ \)

Tam giác SAB cân tại S, O là trung điểm của AB

\( \Rightarrow \widehat {ASO} = \dfrac{{\widehat {ASB}}}{2} = 60^\circ  \Rightarrow SO = \tan 60^\circ .OB = \sqrt 3 .a\sqrt 3  = 3a\)

Thể tích khối nón: \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {\left( {a\sqrt 3 } \right)^2}3a = 3\pi {a^3}\)

Chọn: B