Câu hỏi
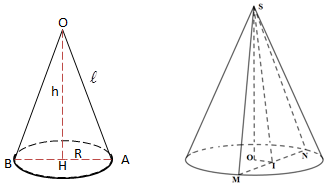
Một hình nón có đỉnh S có bán kính đáy bằng \(a\sqrt 3 \), góc ở đỉnh là \(120^\circ \). Thiết diện qua đỉnh của hình nón là một tam giác. Diện tích lớn nhất \({S_{\max }}\) của thiết diện đó là bao nhiêu?
- A \({S_{\max }} = 2{a^2}\).
- B \({S_{\max }} = 4{a^2}\).
- C \({S_{\max }} = \dfrac{9}{8}{a^2}\).
- D \({S_{\max }} = {a^2}\sqrt 2 \).
Phương pháp giải:
Sử dụng công thức tính diện tích tam giác \({S_{ABC}} = \dfrac{1}{2}AB.AC.\sin \widehat {BAC}\).
Lời giải chi tiết:
Tam giác OAB cân tại O có \(\widehat {AOB} = 120^\circ \Rightarrow \widehat {AOH} = 60^\circ \Rightarrow OA = \dfrac{{HA}}{{\sin 60^\circ }} = \dfrac{{a\sqrt 3 }}{{\dfrac{{\sqrt 3 }}{2}}} = 2a \Rightarrow l = 2a\)
Diện tích thiết diện qua đỉnh : \({S_{OMN}} = \dfrac{1}{2}.SN.SM.\sin \widehat {MSN} = \dfrac{1}{2}.2a.2a.\sin \widehat {MSN} \le \dfrac{1}{2}.2a.2a.\sin 90^\circ = 2{a^2}\)
(Do \(\widehat {MSN} \le 120^\circ \))
Vậy, diện tích lớn nhất \({S_{\max }} = 2{a^2}\) khi và chỉ khi \(\widehat {MSN} = 90^\circ \).
Chọn: A