Câu hỏi
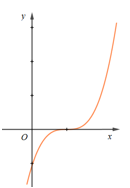
Cho hàm số \(f\left( x \right)\) có đạo hàm \(f'\left( x \right)\) xác định, liên tục trên \(\mathbb{R}\) và \(f'\left( x \right)\) có đồ thị như hình vẽ bên. Khẳng định nào sau đây đúng?
- A Hàm số \(f\left( x \right)\) đồng biến trên \(\left( {1; + \infty } \right)\).
- B Hàm số \(f\left( x \right)\) đồng biến trên \(\left( { - \infty ;1} \right)\).
- C Hàm số \(f\left( x \right)\) đồng biến trên \(\mathbb{R}\).
- D Hàm số \(f\left( x \right)\) đồng biến trên \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\).
Phương pháp giải:
Xác định khoảng \(f'\left( x \right) > 0\).
Lời giải chi tiết:
Quan sát đồ thị hàm số \(y = f'\left( x \right)\) ta thấy \(f'\left( x \right) > 0\) khi \(x \in \left( {1; + \infty } \right) \Rightarrow \) Hàm số \(f\left( x \right)\) đồng biến trên \(\left( {1; + \infty } \right)\).
Chọn: A
Câu hỏi trước
