Câu hỏi
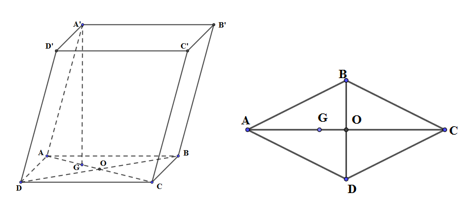
Cho lăng trụ ABCD.A’B’C’D’ có ABCD là hình thoi. Hình chiếu của A’ lên (ABCD) là trọng tâm của tam giác ABD. Tính thể tích khối lăng trụ ABC.A’B’C’ biết \(AB = a,\,\widehat {ABC} = 120^\circ ,\,AA' = a\).
- A \(\dfrac{{{a^3}\sqrt 2 }}{4}\).
- B \(\dfrac{{{a^3}\sqrt 2 }}{6}\).
- C \(\dfrac{{{a^3}\sqrt 2 }}{3}\).
- D \({a^3}\sqrt 2 \).
Phương pháp giải:
Thể tích khối lăng trụ : \(V = Sh\).
Diện tích tam giác đều có các cạnh bằng a là: \(S = \dfrac{{{a^2}\sqrt 3 }}{4}\).
Lời giải chi tiết:
ABCD là hình thoi \( \Rightarrow \Delta ABD\) cân tại A. Mà \(\widehat {ABD} = \dfrac{{\widehat {ABC}}}{2} = \dfrac{{120^\circ }}{2} = 60^\circ \Rightarrow \Delta ABD\) đều
Diện tích tam giác ABC: \({S_{ABC}} = {S_{ABD}} = \dfrac{{{a^2}\sqrt 3 }}{4}\)
Gọi G là trọng tâm tam giác ABD \( \Rightarrow AG = \dfrac{2}{3}AO = \dfrac{2}{3}.\dfrac{{AB.\sqrt 3 }}{2} = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{\sqrt 3 a}}{3}\)
Tam giac A’AG vuông tại G \( \Rightarrow A'G = \sqrt {AA{'^2} - A{G^2}} = \sqrt {{a^2} - {{\left( {\dfrac{{a\sqrt 3 }}{3}} \right)}^2}} = \dfrac{{a\sqrt 6 }}{3}\)
Thể tích khối lăng trụ là: \(V = {S_{ABCD}}.A'G = \dfrac{{{a^2}\sqrt 3 }}{4}.\dfrac{{a\sqrt 6 }}{3} = \dfrac{{{a^3}\sqrt 2 }}{4}\).
Chọn: A