Phương pháp giải:

Thể tích khối lăng trụ : \(V = Sh\).

Lời giải chi tiết:

Ta có: AA’ = A’B = A’D \( \Rightarrow \)Hình chiếu vuông góc của A’ lên (ABD) là tâm đường tròn ngoại tiếp tam giác ABD

Mà ABCD là hình chữ nhật  \( \Rightarrow \) Tam giác ABD vuông tại A \( \Rightarrow \) Tâm đường tròn ngoại tiếp tam giác ABD là trung điểm của BD.

\( \Rightarrow \)Hình chiếu vuông góc của A’ lên (ABD) là trung điểm của BD và cũng là giao điểm O của AC với BD.

Ta có: \(OA = \dfrac{{BD}}{2} = \dfrac{{\sqrt {A{B^2} + A{D^2}} }}{2} = \dfrac{{\sqrt {{a^2} + {{\left( {a\sqrt 3 } \right)}^2}} }}{2} = a\)

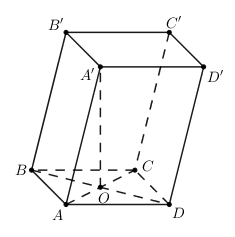
\(A'O \bot \left( {ABCD} \right) \Rightarrow A'O \bot OA \Rightarrow \Delta AOA'\) vuông tại O \( \Rightarrow A'O = \sqrt {AA{'^2} - O{A^2}}  = \sqrt {{{\left( {2a} \right)}^2} - {a^2}}  = a\sqrt 3 \)

Thể tích của khối lăng trụ ABCD.A’B’C’D’ là: \(V = {S_{ABCD}}.OA' = AB.AD.OA' = a.a\sqrt 3 .a\sqrt 3  = 3{a^3}\).

Chọn: D