Câu hỏi
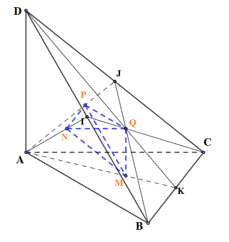
Cho tứ diện ABCD có các cạnh AB, AC, AD đôi một vuông góc với nhau. Gọi M, N, P, Q lần lượt là trọng tâm các mặt ABC, ABD, ACD, BCD. Biết \(AB = 6a,\,AC = 9a,\,AD = 12a\). Thể tích khối tứ diện MNPQ là:
- A \({a^3}\).
- B \(36{a^3}\).
- C \(108{a^3}\)
- D \(4{a^3}\).
Phương pháp giải:
Lập tỉ số thể tích của tứ diện MNPQ với tứ diện ABCD.
Sử dụng công thức đối với tứ diện vuông: \(\dfrac{1}{{{h^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}} + \dfrac{1}{{{c^2}}}\) và \(V = \dfrac{{abc}}{6}\) (với \(a,b,c\) là 3 cạnh góc vuông, h là khoảng cách từ đỉnh vuông đến mặt huyền).
Lời giải chi tiết:
M, N, P lần lượt là trọng tâm các mặt ABC, ABD, ACD
\( \Rightarrow \dfrac{{AN}}{{AI}} = \dfrac{{AP}}{{AJ}} = \dfrac{{AM}}{{AK}} = \dfrac{2}{3}\) \( \Rightarrow \left( {MNP} \right)//\left( {BCD} \right)\) và \(\dfrac{{{S_{MNP}}}}{{{S_{IJK}}}} = \dfrac{4}{9}\).
Mà \(\dfrac{{{S_{IJK}}}}{{{S_{BCD}}}} = \dfrac{1}{4}\,\, \Rightarrow \dfrac{{{S_{MNP}}}}{{{S_{BCD}}}} = \dfrac{1}{9}\)
Gọi h là khoảng cách từ A đến (BCD), h’ là khoảng cách từ Q đến (MNP).
Do \(\left( {MNP} \right)//\left( {BCD} \right) \Rightarrow d\left( {Q;\left( {MNP} \right)} \right) = d\left( {I;\left( {MNP} \right)} \right)\)
Ta có: \(\left\{ \begin{array}{l}AI \cap \left( {MNP} \right) = N\\AN = 2NI\end{array} \right. \Rightarrow d\left( {I;\left( {MNP} \right)} \right) = \dfrac{1}{2}d\left( {A;\left( {MNP} \right)} \right)\)
Lại có: \(\left\{ \begin{array}{l}\left( {MNP} \right)//\left( {BCD} \right)\\AI \cap \left( {MNP} \right) = N\\AI \cap \left( {BCD} \right) = I\\AN = \dfrac{2}{3}AI\end{array} \right. \Rightarrow d\left( {A;\left( {MNP} \right)} \right) = \dfrac{2}{3}d\left( {A;\left( {BCD} \right)} \right) = \dfrac{2}{3}h\)
\( \Rightarrow d\left( {Q;\left( {MNP} \right)} \right) = \dfrac{1}{2}.\dfrac{2}{3}h = \dfrac{1}{3}h \Rightarrow h' = \dfrac{1}{3}h\)
Ta có: \(\dfrac{{{V_{MNPQ}}}}{{{V_{ABCD}}}} = \dfrac{{\dfrac{1}{3}.h'.{S_{MNP}}}}{{\dfrac{1}{3}.h.{S_{BCD}}}} = \dfrac{{h'}}{h}.\dfrac{{{S_{MNP}}}}{{{S_{BCD}}}} = \dfrac{1}{3}.\dfrac{1}{9} = \dfrac{1}{{27}}\)
Mà \({V_{ABCD}} = \dfrac{{AB.AC.AD}}{6} = \dfrac{{6a.9a.12a}}{6} = 108{a^3}\) (do ABCD là tứ diện vuông tại đỉnh A)
\( \Rightarrow {V_{MNPQ}} = \dfrac{1}{{27}}.108{a^3} = 4{a^3}\).
Chọn: D







