Câu hỏi
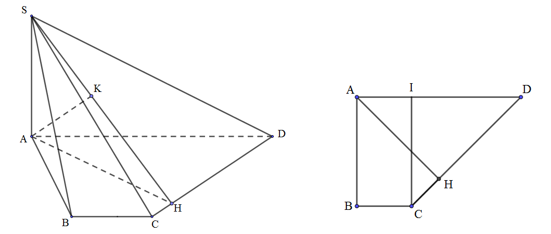
Cho hình chóp tứ giác \(S.ABCD\) có \(SA \bot \left( {ABCD} \right)\), \(ABCD\) là hình thang vuông tại A và B, biết \(AB = 2a\), \(AD = 3BC = 3a\), khoảng cách từ A đến mặt phẳng \(\left( {SCD} \right)\) bằng \(\dfrac{{3\sqrt 6 }}{4}a\).Thể tích khối chóp \(S.ABCD\) là:
- A \(2\sqrt 6 {a^3}\).
- B \(2\sqrt 3 {a^3}\).
- C \(6\sqrt 3 {a^3}\).
- D \(6\sqrt 6 {a^3}\).
Phương pháp giải:
Thể tích khối chóp: \(V = \dfrac{1}{3}Sh\).
Lời giải chi tiết:
Dựng \(AH \bot CD\) tại H, \(AK \bot SH\) tại K. Ta có: \(\left\{ \begin{array}{l}CD \bot AH\\CD \bot SA\end{array} \right. \Rightarrow CD \bot \left( {SAH} \right) \Rightarrow CD \bot AK\)
Mà \(AK \bot SH \Rightarrow AK \bot \left( {SCD} \right) \Rightarrow d\left( {A;\left( {SCD} \right)} \right) = AK = \dfrac{{3\sqrt 6 }}{4}a\)
Dựng \(CI \bot AD\) tại I \( \Rightarrow \)\(ABCI\) là hình chữ nhật có \(AI = BC = a,\,\,IC = AB = 2a\,\, \Rightarrow ID = IC = 2a\)
\( \Rightarrow \Delta ICD\) vuông cân tại I \( \Rightarrow \widehat D = 45^\circ \,\, \Rightarrow \Delta AHD\) vuông cân tại H\( \Rightarrow AH = \dfrac{{AD}}{{\sqrt 2 }} = \dfrac{{3a}}{{\sqrt 2 }}\)
\(\Delta SAH\) vuông tại A có \(AK \bot SH \Rightarrow \dfrac{1}{{S{A^2}}} + \dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{K^2}}} \Leftrightarrow \dfrac{1}{{S{A^2}}} = \dfrac{1}{{{{\left( {\dfrac{{3a}}{{\sqrt 2 }}} \right)}^2}}} - \dfrac{1}{{{{\left( {\dfrac{{3\sqrt 6 }}{4}a} \right)}^2}}} = \dfrac{2}{{27{a^2}}} \Rightarrow SA = \dfrac{{3\sqrt 6 a}}{2}\)
ABCD là hình thang vuông tại A và B \({S_{ABCD}} = \dfrac{1}{2}\left( {AD + BC} \right).AB = \dfrac{1}{2}.\left( {3a + a} \right).2a = 4{a^2}\)
\(SA \bot \left( {ABCD} \right) \Rightarrow {V_{S.ABCD}} = \dfrac{1}{3}.{S_{ABCD}}.SA = \dfrac{1}{3}.\dfrac{{3\sqrt 6 a}}{2}.4{a^2} = 2\sqrt 6 {a^3}\).
Chọn: A