Phương pháp giải:

Vẽ đồ thị hàm số và nhận xét.

Lời giải chi tiết:

Xét hàm số \(y = {x^3} - 4{x^2} + 3\), có: \(y' = 3{x^2} - 8x\), \(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \dfrac{8}{3}\end{array} \right.\)

Hàm số \(y = {x^3} - 4{x^2} + 3\) đạt cực trị tại \(x = 0\) và \(x = \dfrac{8}{3}\)

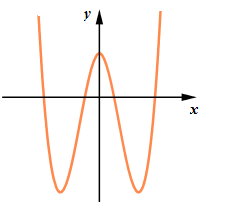
Do đồ thị của hàm số \(y = {\left| x \right|^3} - 4{x^2} + 3\) được dựng từ đồ thị hàm số \(y = {x^3} - 4{x^2} + 3\,\,\left( C \right)\) bằng cách giữ nguyên đồ thị (C) nằm bên phải trục tung và lấy đối xứng phần đồ thị này qua trục tung, do đó đồ thị hàm số như sau:

Dựa vào đồ thị hàm số ta thấy số cực trị của đồ thị hàm số \(y = {\left| x \right|^3} - 4{x^2} + 3\) là 3.

Chọn: A