Phương pháp giải:

Gọi I là trực tâm tam giác ABC, chứng minh \(IH \bot \left( {SBC} \right)\).

Lời giải chi tiết:

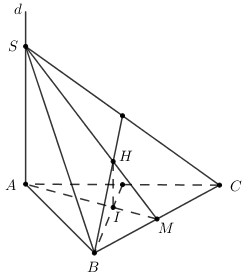
Gọi I là trực tâm của tam giác ABC, M là trung điểm của BC ta có:

\(\left\{ \begin{array}{l}AM \bot BC\\SA \bot BC\end{array} \right. \Rightarrow BC \bot \left( {SAM} \right) \Rightarrow BC \bot SM \Rightarrow H \in SM;\,\,BC \bot IH\).

Ta có \[(\left\{ \begin{array}{l}BH \bot SC\\BI \bot SC\end{array} \right. \Rightarrow SC \bot \left( {BIH} \right) \Rightarrow SC \bot IH\)

Do đó \(\left\{ \begin{array}{l}IH \bot BC\\IH \bot SC\end{array} \right. \Rightarrow IH \bot \left( {SBC} \right) \Rightarrow IH \bot SM \Rightarrow \widehat {IHM} = {90^0}\). Do \(\Delta ABC\) cố định \( \Rightarrow I,M\) cố định \( \Rightarrow \) H thuộc đường tròn đường kinh IM. Khi đó mặt cầu chứa đường tròn đường kính IM có bán kính nhỏ nhất bằng \(\frac{{IM}}{2}\).

Xét tam giác ABC đều \( \Rightarrow \) trực tâm I đồng thời là trọng tâm \( \Rightarrow IM = \frac{1}{3}AM = \frac{1}{3}\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{6}\).

Vậy \({R_{\min }} = \frac{{IM}}{2} = \frac{{a\sqrt 3 }}{{12}}\).

Chọn C.