Phương pháp giải:

+) Cách 1: Sử dụng chức năng MODE 7 của máy tính để bấm máy, tìm GTNN của hàm số trên đoạn đã cho.

+) Cách 2: Khảo sát hàm số \(y = f\left( x \right),\;\) tính các giá trị tại các mút của đoạn cần tìm GTNN để chọn đáp án đúng.

Lời giải chi tiết:

Điều kiện: \(x \ne  - 1.\)

Vì \( - 1 \notin \left[ {0;\;3} \right]\) nên với bài toán này ta có thể chọn cách bấm máy tính để làm nhanh hơn.

Cách 1: Ta sử dụng máy tính để bấm máy:

+) Bước 1: Nhập hàm số \(y = \dfrac{{x - 1}}{{x + 1}}\) vào máy tính

+) Bước 2: Start = 0, End = 3, Step \( = \dfrac{{3 - 0}}{{19}}.\)

Khi đó ta được: 

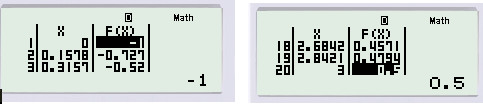
Ta thấy giá trị của hàm số luôn tăng từ -1 đến 0,5.

Vậy \(\mathop {\min }\limits_{x \in \left[ {0;\;3} \right]} y =  - 1\) khi \(x = 0.\)

Chọn C.