Câu hỏi
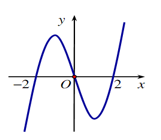
Cho hàm số \(f\left( x \right)\) xác định trên R và có đồ thị hàm số \(y = f'\left( x \right)\) là đường cong trong hình bên. Mệnh đề nào dưới đây đúng?
- A Hàm số \(f\left( x \right)\) đồng biến trên khoảng \(\left( {1;2} \right)\).
- B Hàm số \(f\left( x \right)\) đồng biến trên khoảng \(\left( { - 2;1} \right)\).
- C Hàm số \(f\left( x \right)\) nghịch biến trên khoảng \(\left( { - 1;1} \right)\).
- D Hàm số \(f\left( x \right)\) nghịch biến trên khoảng \(\left( {0;2} \right)\).
Phương pháp giải:
Cho hàm số \(y = f\left( x \right)\).
Hàm số đồng biến (nghịch biến) trên \(\left( {a;b} \right) \Leftrightarrow f'\left( x \right) \ge 0\,\,\left( {f'\left( x \right) \le 0} \right)\,\,\forall x \in \left( {a;b} \right)\) và bằng 0 tại hữu hạn điểm.
Lời giải chi tiết:
Dựa vào đồ thị hàm số \(y = f'\left( x \right)\) ta có \(\left\{ \begin{array}{l}f'\left( x \right) > 0 \Leftrightarrow x \in \left( { - 2;0} \right) \cup \left( {2; + \infty } \right)\\f'\left( x \right) > 0 \Leftrightarrow x \in \left( { - \infty ; - 2} \right) \cup \left( {0;2} \right)\end{array} \right.\) , do đó hàm số \(y = f\left( x \right)\) đồng biến trên \(\left( { - 2;0} \right)\) và \(\left( {2; + \infty } \right)\), nghịch biến trên \(\left( { - \infty ; - 2} \right)\) và \(\left( {0;2} \right)\).
Chọn D.