Phương pháp giải:

Khảo sát hàm số \(y = f\left( x \right)\), lập bảng biến thiên và kiểm chứng mệnh đề.

Lời giải chi tiết:

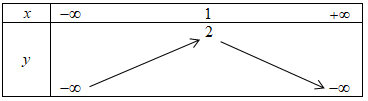
+ Ta có bảng biến thiên của hàm số \(y =  - {x^2} + 2x + 1\) như sau:

Dựa vào BBT ta thấy đồ thị hàm số có đỉnh là \(I\left( {1;\;2} \right)\) và có trục đối xứng là đường thẳng \(x = 1.\)

\( \Rightarrow \) đáp án A và C sai.

Hàm số nghịch biến trên khoảng \(\left( {1; + \infty } \right)\)

Ta có: \(1 < {2^{2017}} < {3^{2017}} \Rightarrow f\left( {{2^{2017}}} \right) > f\left( {{3^{2017}}} \right)\)

Chọn D.