Câu hỏi
Một vật chuyển động thẳng biến đổi đều trên mặt phẳng ngang từ trạng thái đứng yên.
Sau 2s kể từ lúc bắt đầu chuyển động, vật đạt tốc độ 3m/s. Cho g = 10 m/s2.
a. Tính độ lớn gia tốc của chuyển động ?
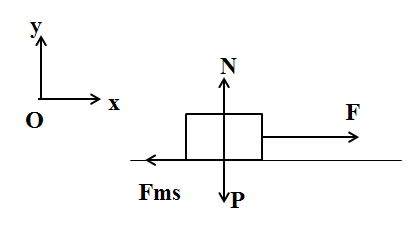
b. Biết vật có khối lượng 2kg được kéo bằng lực \(\overrightarrow{F}\) nằm ngang, có độ lớn F = 7 N. Biết chuyển động của vật trượt trên mặt phẳng ngang có ma sát trượt. Vẽ hình biểu diễn các lực tác dụng lên vật và tính hệ số ma sát trượt giữa vật và sàn ?
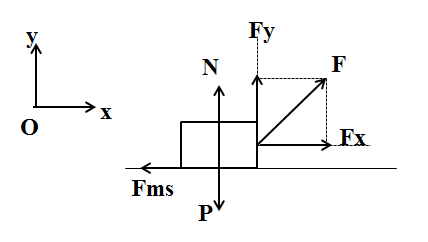
c. Để vật chuyển động thẳng đều người ta kéo vật bằng lực \({{\overrightarrow{F}}_{1}}\) nghiêng chếch lên trên và hợp với mặt phẳng ngang góc α (với sinα = 0,6). Tìm độ lớn của lực F1?
- A a) 1,2m/s2; b) 0,1; c) 3N
- B a) 1,2m/s2; b) 0,4; c) 3N
- C a) 1,25m/s2; b) 0,1; c) 3,2N
- D a) 1,5m/s2; b) 0,2; c) 7,7N
Phương pháp giải:
- Vận tốc tức thời : v = v0 + at
- Định luật 2 Niu tơn: \(\overrightarrow{F}=m\overrightarrow{a}\)
- Lực ma sát giữa vật và sàn: Fms = µN
- Vật chuyển động thẳng đều thì hợp lực tác dụng bằng 0
Lời giải chi tiết:
a)
Ta có: v0 = 0; t = 2s; v = 3m/s
Gia tốc của vật: \(\;v = {v_0} + at \Rightarrow 3 = 2a \Rightarrow a = 1,5m/{s^2}\)
b)
Áp dụng định luật 2 Niu tơn: \(\vec P + \vec N + \vec F + \overrightarrow {{F_{ms}}} = m\vec a\)
Chiếu biểu thức trên lên trục Oy ta được: \( - P + N = 0 \Rightarrow N = P = mg\)
Chiếu biểu thức trên lên trục Ox ta được:
\(F - {F_{ms}} = ma \Leftrightarrow F - \mu N = ma \Rightarrow F - \mu mg = ma \Rightarrow 7 - \mu .2.10 = 2.1,5 \Rightarrow \mu = 0,2\)
c)
Áp dụng định luật 2 Niu tơn:
\(\vec P + \vec N + {\vec F_1} + \overrightarrow {{F_{ms}}} = m\vec a\)
Chiếu biểu thức trên lên trục Oy ta được: \(N-P + Fsin\alpha = 0 \Rightarrow N = mg - Fsin\alpha \)
Chiếu biểu thức trên lên trục Ox ta được:
\({F_1}cos\alpha --{F_{ms}} = ma \Rightarrow {F_1}.cos\alpha - \mu N = ma \Rightarrow {F_1}.cos\alpha --0,2.(2.10 - 7.sin\alpha ) = 2.1,5\)
Với sinα = 0,6 thì cosα = 0,8
Thay vào ta được F1 = 7,7N