Phương pháp giải:

: a) Dùng phương trình độc lập với thời gian :

\({v^2} - v_0^2 = 2as\)

 để tìm gia tốc a.

 Vẽ hình biểu diễn các lực tác dụng lên xe trên hệ trục tọa độ Oxy: lực của động cơ, lực ma sát, trọng lực, phản lực N. Dùng định luật II Niu – Tơn:  

\(\sum {\overrightarrow F } = m.\overrightarrow a \)

. Sau đó chiếu phương trình định luật II lên các trục tọa độ. Và tìm F.

b) Khi lực F ngừng tác dụng, chỉ còn lực ma sát, trọng lực và phản lực. Vẽ hình vật trên mặt phẳng nghiêng, Dùng định luật II Niu – Tơn:  \(\sum {\overrightarrow F } = m.\overrightarrow a \)

. Sau đó chiếu phương trình định luật II lên các trục tọa độ. Và tìm gia tốc mới.

Dùng phương trình độc lập với thời gian : \({v^2} - v_0^2 = 2as\) để tìm quãng đường vật đi được đến khi dừng lại.

Sau đó tìm độ cao vật đạt được h = s.sinα

Lời giải chi tiết:

Đổi 14,4 km/h = 4m/s.

Gia tốc a của vật là 

\({v^2} - v_0^2 = 2as \Leftrightarrow a = \frac{{{4^2} - 0}}{{2.8}} = 1m/{s^2}\)

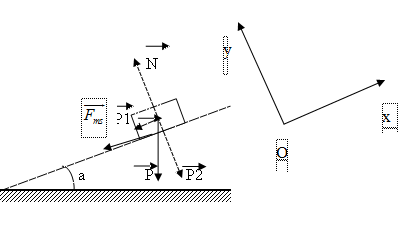
Ta có hình vẽ

Chọn hệ quy chiếu gắn với mặt đất, các lực tác dụng lên vật như trên hình vẽ 

 Vật chuyển động thẳng với gia tốc = 1 m/s², theo định luật I và II Niu – tơn ta có

\(\overrightarrow F + \overrightarrow P + \overrightarrow N + \overrightarrow {{F_{ms}}} = m.\overrightarrow a \)

Chiếu lên hai trục Ox, Oy ta được

\(\left\{ \begin{array}{l}
{\rm{Ox: F - }}{{\rm{F}}_{ms}} = m.a\\
Oy:P - N = 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
{\rm{Ox; F = }}{{\rm{F}}_{ms}} + ma = \mu .N + ma = 0,2.50 + 5.1 = 15N\\
Oy:P = N = m.g = 5.10 = 50N
\end{array} \right.\)

Vậy lực của động cơ là 15 N

b) Bây giờ vật chuyển động trên mặt phẳng nghiêng

Ta có hình vẽ

\(\overrightarrow P + \overrightarrow N + \overrightarrow {{F_{ms}}} = m.\overrightarrow {a'} \)

Chiếu lên hai trục Ox, Oy ta được

\(\begin{array}{l}
\left\{ \begin{array}{l}
{\rm{Ox: - F}}{{\rm{'}}_{ms}} - {P_1} = m.a'\\
Oy:{P_2} - N = 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
{\rm{Ox; - F}}{{\rm{'}}_{ms}} - P.\sin \alpha = - \mu .N - mg.\sin {15^0} = ma'\\
Oy:P.\cos \alpha = N = m.g.\cos {15^0} = 5.10.\cos {15^0} = 48,3N
\end{array} \right.\\
\Leftrightarrow - 0,1.48,3 - 50.\sin {15^0} = 5.a' \Leftrightarrow a' = - 3,55m/{s^2}
\end{array}\)

Vậy xe chuyển động chậm dần đều với gia tốc a = -3,55 m/s².

Quãng đường xe đi được đến khi dừng lại là s, được xác định bởi

\(\begin{array}{l}
{v^2} - v_0^2 = 2a's\\
\Leftrightarrow s = \frac{{{v^2} - v_0^2}}{{2a'}} = \frac{{0 - {4^2}}}{{2.( - 3,55)}} = 2,25m
\end{array}\)

Vậy vật đi được 2,25 m trước khi dừng hẳn;

Độ cao mà vật đạt được là  

\(h = s.\sin {15^0} = 2,25.\sin {15^0} = 0,58m\)