Phương pháp giải:

Cách 1: Sử dụng công thức: \(A_n^k = \frac{{n!}}{{(n - k)!}}\)

Với \(k = 2\)  thay vào biểu thức rút gọn. Từ đó giải \(x.\)

Cách 2: Sử dụng máy tính:

+) Thay các giá trị của \(x\) ở mỗi đáp án vào máy tính và bấm máy, đáp án nào ra đúng giá trị bài cho thì chọn đáp án đó.

Lời giải chi tiết:

Cách 1: Sử dụng công thức:

Điều kiện: \(x \in N,x \ge 2\).

Ta có:\(A_n^k = \frac{{n!}}{{(n - k)!}} \Rightarrow A_x^2 = 110 \Leftrightarrow \frac{{x!}}{{\left( {x - 2} \right)!}} = 110 \Leftrightarrow x(x - 1) = 110 \Leftrightarrow \left[ \begin{array}{l}x = 11\\x =  - 10\end{array} \right.\).

So sánh điều kiện ta nhận \(x = 11\).

Cách 2: Sử dụng máy tính:

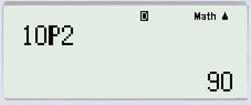
+) Thử với đáp án A và bấm máy ta được: 

Ta thấy: \(A_{10}^2 = 90 \ne 110 \Rightarrow \) loại đáp án A.

+) Thử với đáp án B và bấm máy ta được: 

Ta thấy: \(A_{11}^2 = 110 \Rightarrow \) chọn  đáp án B.

Chọn B