Phương pháp giải:

Áp dụng đầy đủ các bước lập BBT của đồ thị hàm số \(y = a{x^2} + bx + c\)

Lời giải chi tiết:

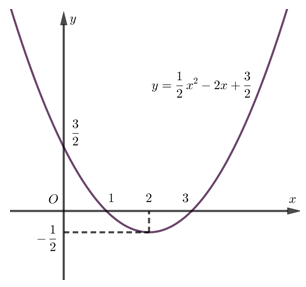
Vẽ parabol  \(y = \frac{1}{2}{x^2} - 2x + \frac{3}{2}\)

+ Tập xác định \(D = R\).

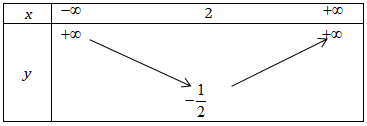
+ Bảng biến thiên:

+ Vẽ đồ thị hàm số:

+ Đỉnh \(I\left( {2; - \frac{1}{2}} \right)\)

+ Trục đối xứng \(x = 2\)

+ Giao với trục tung \(A\left( {0;\frac{3}{2}} \right)\)

+ Giao với trục hoành tại \(B\left( {1;0} \right);\,\,B'\left( {3;0} \right)\).

Dựa vào đồ thị ta có để \(\left( P \right)\) nằm phía dưới trục Ox thì \(1 < x < 3\)

Chọn A.

Phương pháp giải:

M thuộc \(\left( C \right)\) gọi tọa độ điểm M, tìm giá trị nhỏ nhất của AM  từ đó suy ra điểm M.

Lời giải chi tiết:

TXĐ: \(D = \left[ { - \sqrt 5 ;\sqrt 5 } \right]\)

Điểm M thuộc \(\left( C \right)\) nên \(M\left( {a;\sqrt {5 - {a^2}} } \right)\)

\(\begin{array}{l} \Rightarrow A{M^2} = {\left( {a - 2} \right)^2} + {\left( {\sqrt {5 - {a^2}}  - 4} \right)^2} = {a^2} - 4a + 4 + 5 - {a^2} - 8\sqrt {5 - {a^2}}  + 16\\\;\;\;\;\;\;\;\;\;\;\; = 25 - 4\left( {a + 2\sqrt {5 - {a^2}} } \right).\end{array}\)

Chứng minh: \(a + 2\sqrt {5 - {a^2}}  \le 5\;\;\left( * \right)\) ta có:

\(\begin{array}{l}\left( * \right) \Leftrightarrow 2\sqrt {5 - {a^2}}  \le 5 - a \Leftrightarrow 4\left( {5 - {a^2}} \right) \le 25 - 10a + {a^2}\\ \Leftrightarrow 20 - 4{a^2} \le 25 - 10a + {a^2}\\ \Leftrightarrow 5{a^2} - 10a + 5 \ge 0\\ \Leftrightarrow {\left( {a - 1} \right)^2} \ge 0\;\;\forall a \in \left[ { - \sqrt 5 ;\;\sqrt 5 } \right].\\ \Rightarrow AM \ge \sqrt 5 .\end{array}\) 

Dấu ‘=’ xảy ra \( \Leftrightarrow a = 1 \Rightarrow M\left( {1;2} \right)\) 

Chọn D.