Phương pháp giải:

a) Áp dụng đầy đủ các bước lập BBT của đồ thị hàm số \(y = ax + b\).

b) Tìm điều kiện để phương trình có 2 nghiệm.

Lời giải chi tiết:

Cho hàm số \(y = (m - 2){x^2} + 3x + 3\) (1).

a) Lập bảng biến thiên, vẽ đồ thị hàm số (1) khi\(m = 2\).

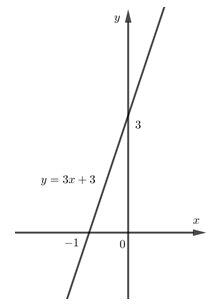
    Khi \(m = 2\) ta có hàm số: \(y = 3x + 3\)

+) Bảng biến thiên:

+) Đồ thị: đồ thị là đường thẳng đi qua hai điểm : \(\left( {0;3} \right)\) và \(\left( { - 1;0} \right)\).

b) Tìm các giá trị của m để đồ thị hàm số (1) cắt trục hoành tại hai điểm phân biệt.

Đồ thị hàm số \(y = (m - 2){x^2} + 3x + 3\) cắt trục hoành tại hai điểm phân biệt khi và chỉ khi phương trình \((m - 2){x^2} + 3x + 3 = 0\) có hai nghiệm phân biệt hay :

\(\left\{ \begin{array}{l}m \ne 2\\\Delta  = {3^2} - 4(m - 2).3 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne 2\\ - 12m + 33 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne 2\\m < \frac{{33}}{{12}}\end{array} \right..\)

Vậy phương trình có hai nghiệm phân biệt khi \(m < \frac{{33}}{{12}},\;m \ne 2.\)

Chọn A.