Phương pháp giải:

Khoảng cách giữa hai đường thẳng bằng độ dài đoạn vuông góc chung của hai đường thẳng đó.

Lời giải chi tiết:

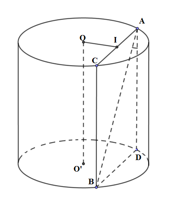
Gọi C, D lần lượt là hình chiếu vuông góc của A, B lên mặt phẳng đáy còn lại (như hình vẽ). I là trung điểm của AC.

\(\begin{array}{l}OO'//AD \Rightarrow OO'//\left( {ACBD} \right)\\ \Rightarrow d\left( {OO';AB} \right) = d\left( {OO';\left( {ACBD} \right)} \right) = d\left( {O;\left( {ACBD} \right)} \right)\,\,(1)\end{array}\)

Ta có:\(\left\{ \begin{array}{l}AD//OO'\\OO' \bot \left( {OAC} \right)\end{array} \right. \Rightarrow AD \bot \left( {OAC} \right) \Rightarrow AD \bot OI\)

Mà \(AC \bot OI\,\, \Rightarrow OI \bot \left( {ACBD} \right) \Rightarrow d\left( {O;\left( {ACBD} \right)} \right) = OI\) (2)

Từ (1), (2) \( \Rightarrow d\left( {AB;OO'} \right) = OI\)

Tam giác ABD vuông tại D, có \(\widehat {BAD} = \widehat {\left( {AB;AD} \right)} = \widehat {\left( {AB;OO'} \right)} = 30^\circ \)

\( \Rightarrow BD = AD.\tan 30^\circ  = 25.\dfrac{1}{{\sqrt 3 }} = \dfrac{{25}}{{\sqrt 3 }} \Rightarrow AC = BD = \dfrac{{25}}{{\sqrt 3 }}\,\, \Rightarrow IA = \dfrac{1}{2}AC = \dfrac{{25}}{{2\sqrt 3 }}\)

Tam giác OIA vuông tại I \( \Rightarrow OI = \sqrt {O{A^2} - I{A^2}}  = \sqrt {{{20}^2} - {{\left( {\dfrac{{25}}{{2\sqrt 3 }}} \right)}^2}}  = \dfrac{{5\sqrt {501} }}{6}\,\, \Rightarrow d = \dfrac{{5\sqrt {501} }}{6}\) .

Chọn: B