Câu hỏi
Một khối đồ chơi gồm hai khối trụ \(\left( {{H_1}} \right),\,\,\left( {{H_2}} \right)\) xếp chồng lên nhau, lần lượt có bán kính đáy và chiều cao tương ứng là \({r_1},\,\,{h_1},\,\,{r_2},\,\,{h_2}\) thỏa mãn \({r_2} = \dfrac{1}{2}{r_1},\,\,{h_2} = 2{h_1}\) (tham khảo hình vẽ). Biết rằng thể tích của toàn bộ khối đồ chơi bằng \(30c{m^3}\) . Tính thể tích khối trụ \(\left( {{H_1}} \right)\) bằng:
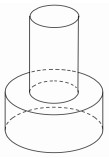
- A \(24c{m^3}\)
- B \(15c{m^3}\)
- C \(20c{m^3}\)
- D \(10c{m^3}\)
Phương pháp giải:
Áp dụng công thức tính thể tích khối trụ \(V = \pi {r^2}h\) trong đó r là bán kính của khối trụ; h là chiều cao của khối trụ.
Sử dụng đề bài để tính thể tích toàn bộ khối đồ chơi từ đó tìm được thể tích của khối trụ (H1).
Lời giải chi tiết:
Thể tích của toàn bộ khối đồ chơi là:
\(\begin{array}{l}V = \pi r_1^2{h_1} + \pi r_2^2{h_2} = \pi r_1^2{h_1} + \pi \dfrac{1}{4}r_1^2.2{h_1} = \dfrac{3}{2}\pi r_1^2{h_1} = 30\\ \Rightarrow \pi r_1^2{h_1} = 20\end{array}\)
Vậy thể tích khối trụ (H1) là 20 cm3.
CHỌN C.







