Phương pháp giải:

Sử dụng phương pháp vecto quay (mối quan hệ giữa dao động điều hòa và chuyển động tròn đều).

Lời giải chi tiết:

tại thời điểm ban đầu vật đang ở vị trí

\(\varphi = \frac{\pi }{3}\)

Chu kỳ dao động của vật là: T = 0,5s.

Khoảng thời gian

\(\begin{array}{l}
\Delta t = \frac{7}{{24}}s = \frac{7}{{24.0,5}}T = \frac{7}{{12}}T\\
= > \alpha = \frac{7}{{12}}.2\pi = \frac{{7\pi }}{6}rad
\end{array}\)

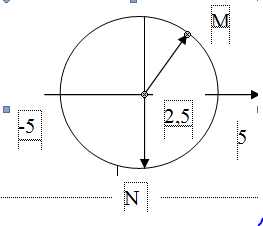
Vậy các vị trí ban đầu và cuối của khoảng thời gian ta xét là các vị trí M, N trên đường tròn, được biểu diễn như hình sau

Vậy quãng đường mà vật đã đi được là : S = 2,5 + 5 + 5 = 12,5 cm