Câu hỏi
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có tâm \(I\). Gọi \(V,\,\,{V_1}\) lần lượt là thể tích của khối hộp \(ABCD.A'B'C'D'\) và khối chóp \(I.ABCD\). Tính tỉ số \(k = \dfrac{{{V_1}}}{V}\).
- A \(k = \dfrac{1}{6}\).
- B \(k = \dfrac{1}{3}\).
- C \(k = \dfrac{1}{8}\).
- D \(k = \dfrac{1}{{12}}\).
Phương pháp giải:
Xác định tỉ số chiều cao và tỉ số diện tích đáy của chóp I.ABCD và khối hộp ABCD.A’B’C’D’.
Lời giải chi tiết:
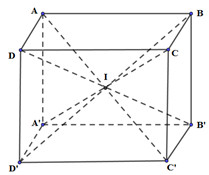
\({V_1} = \dfrac{1}{3}.d\left( {I;\left( {ABCD} \right)} \right).{S_{ABCD}} = \dfrac{1}{3}.\dfrac{1}{2}.d\left( {A;\left( {ABCD} \right)} \right).{S_{ABCD}}\)
(do I là trung điểm của AC)
\( = \dfrac{1}{6}.AA'.{S_{ABCD}} = \dfrac{1}{6}V\,\, \Rightarrow k = \dfrac{{{V_1}}}{V} = \dfrac{1}{6}\).
Chọn: A
Câu hỏi trước
